题目内容
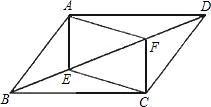
如图，E、F是平行四边形ABCD的对角线AC上的两点，AE=CF．求证：DE=BF．
【答案】分析：连接BE，DF，BD，BD交AC于O，根据平行四边形性质求出OA=OC，OD=OB，推出OE=OF，根据平行四边形的判定推出四边形BEDF是平行四边形即可．
解答：
证明：连接BE，DF，BD，BD交AC于O，
∵四边形ABCD是平行四边形，
∴OA=OC，OD=OB，
∵AE=CF，
∴OE=OF，
∴四边形BEDF是平行四边形，
∴DE=BF．
点评：本题考查了平行四边形的性质和判定等应用，关键是能熟练地运用平行四边形的性质和判定进行推理，此题的证明方法二是证△AED≌△CFB，推出DE=BF．
解答：
证明：连接BE，DF，BD，BD交AC于O，∵四边形ABCD是平行四边形，
∴OA=OC，OD=OB，
∵AE=CF，
∴OE=OF，
∴四边形BEDF是平行四边形，
∴DE=BF．
点评：本题考查了平行四边形的性质和判定等应用，关键是能熟练地运用平行四边形的性质和判定进行推理，此题的证明方法二是证△AED≌△CFB，推出DE=BF．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
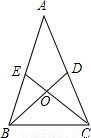
8、
1、如图，在△ABC中，D、E分别是AC、AB上的点，BD与CE交于点O，给出下列四个条件：①∠EBO=∠DCO；②∠BEO=∠CDO；③BE=CD；④OB=OC．
相交于点C．
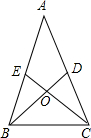1、如图，在△ABC中，D、E分别是AC、AB上的点，BD与CE交于点O，给出下列四个条件：①∠EBO=∠DCO；②∠BEO=∠CDO；③BE=CD；④OB=OC．
