题目内容
 如图所示,两个边长为2的正方形有两条边分别落在两条坐标轴上,一个顶点与原点O重合,双曲线y=
如图所示,两个边长为2的正方形有两条边分别落在两条坐标轴上,一个顶点与原点O重合,双曲线y=| k |
| x |
| A、1 | B、2 | C、4 | D、6 |
分析:由于双曲线y=
的两支分别经过这两个正方形的对角线的交点A,B,由此确定A和B的坐标,那么两扇形的半径和圆心角都相等,扇形的面积就相等,所以利用的正方形面积公式即可求出阴影部分的面积.
| k |
| x |
解答:解:∵双曲线y=
的两支分别经过这两个正方形的对角线的交点A,B,
∴点A(1,1),B(-1,-1),
∴两扇形的半径和圆心角都相等,扇形的面积就相等,
∴阴影部分的面积之和等于正方形的面积=2×2=4.
故选C.
| k |
| x |
∴点A(1,1),B(-1,-1),
∴两扇形的半径和圆心角都相等,扇形的面积就相等,
∴阴影部分的面积之和等于正方形的面积=2×2=4.
故选C.
点评:解决本题的关键是读懂题意,然后求出A、B两点坐标,最后得到阴影部分的面积的求法.

练习册系列答案
相关题目
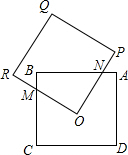 如图所示,两个边长都为2的正方形ABCD和OPQR,如果O点正好是正方形ABCD的中心,而正方形OPQR可以绕O点旋转,那么它们重叠部分的面积为( )
如图所示,两个边长都为2的正方形ABCD和OPQR,如果O点正好是正方形ABCD的中心,而正方形OPQR可以绕O点旋转,那么它们重叠部分的面积为( ) 如图所示,两个边长为2的正方形有两条边分别落在两条坐标轴上,一个顶点与原点O重合,双曲线y=
如图所示,两个边长为2的正方形有两条边分别落在两条坐标轴上,一个顶点与原点O重合,双曲线y= 的两支分别经过这两个正方形的对角线的交点A,B,则图中阴影部分的面积之和是
的两支分别经过这两个正方形的对角线的交点A,B,则图中阴影部分的面积之和是 的两支分别经过这两个正方形的对角线的交点A,B,则图中阴影部分的面积之和是( )
的两支分别经过这两个正方形的对角线的交点A,B,则图中阴影部分的面积之和是( )
 的两支分别经过这两个正方形的对角线的交点A,B,则图中阴影部分的面积之和是( )
的两支分别经过这两个正方形的对角线的交点A,B,则图中阴影部分的面积之和是( )