题目内容
ABCD为平行四边形，过A作AE⊥BD，过C作CF⊥BD，若∠ADE=30°，BE=EF=
，则四边形ABCD的面积为________．
6
分析：易证△ABE≌△CDF，可得BE=DF，即可求得DE的长度，根据DE和∠ADE即可求得AE的长度，根据BD、AE即可计算△ABD的面积，根据△ABD的面积即可计算平行四边形ABCD的面积．
解答：∵∠AEB=∠CFD，∠ABE=∠CDF，AB=CD，
∴△ABE≌△CDF，
∴BE=DF，∴BD=3，
∵∠ADE=30°，
∴AE=
DE=（EF+DF）=2，
∴△ABD的面积为
BD•AE=×3×2=3，
∴四边形ABCD的面积等于△ABD的面积的2倍，
∴四边形ABCD的面积=2×3=6．
故答案为 6．
点评：本题考查了全等三角形的证明和全等三角形对应边相等的性质，勾股定理在直角三角形中的运用，本题中正确计算△ABD的面积是解题的关键．
分析：易证△ABE≌△CDF，可得BE=DF，即可求得DE的长度，根据DE和∠ADE即可求得AE的长度，根据BD、AE即可计算△ABD的面积，根据△ABD的面积即可计算平行四边形ABCD的面积．
解答：∵∠AEB=∠CFD，∠ABE=∠CDF，AB=CD，
∴△ABE≌△CDF，
∴BE=DF，∴BD=3
，∵∠ADE=30°，
∴AE=
DE=（EF+DF）=2，∴△ABD的面积为
BD•AE=×3×2=3，∴四边形ABCD的面积等于△ABD的面积的2倍，
∴四边形ABCD的面积=2×3
=6．故答案为 6
．点评：本题考查了全等三角形的证明和全等三角形对应边相等的性质，勾股定理在直角三角形中的运用，本题中正确计算△ABD的面积是解题的关键．
练习册系列答案
相关题目
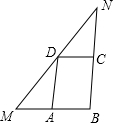已知四边形ABCD为平行四边形，经过点D作直线MN，分别交BA、BC的延长线于点M、N，且∠NDC=∠MDA，若四边形ABCD的周长是4，则MB的长是
（2011•资阳）如图，已知四边形ABCD为平行四边形，AE⊥BD于E，CF⊥BD于F．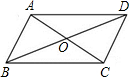
如图，在四边形ABCD中，AC与BD相交于点O，如果只给出条件“AB∥CD”，还不能判定四边形ABCD为平行四边形，若想使四边形ABCD为平行四边形，要添加一个条件，这个条件可以是（ ）