题目内容
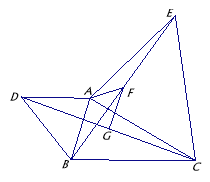
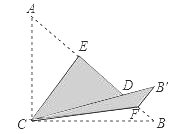
【题目】如图,Rt△ABC中,∠ACB=90°,![]() ,
,![]() ,将边
,将边![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在
落在![]() 上的点
上的点![]() 处;再将边
处;再将边![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在
落在![]() 的延长线上的点
的延长线上的点![]() 处,两条折痕与斜边
处,两条折痕与斜边![]() 分别交于点
分别交于点![]() 、
、![]() ,则线段
,则线段![]() 的长为( )
的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
根据折叠的性质可知AC=CD,∠A=∠CDE,CE⊥AB,Rt△ABC中根据勾股定理求得AB=5,进而证得△ABC∽△DB′F,由三角形相似的性质即可求得B′F的长.
∵Rt△ABC中,∠ACB=90°,AC=3,BC=4,∴AB=5,根据折叠的性质可知AC=CD,∠A=∠CDE,CE⊥AB,∴B′D=BC﹣CD=4﹣3=1.
∵∠B′DF=∠CDE,∴∠A=∠B′DF.
∵∠B=∠B′,∴△ABC∽△DB′F,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴B′F=
,∴B′F=![]() .
.
故选B.

练习册系列答案
相关题目
【题目】求一个正数的算术平方根,有些数可以直接求得,如![]() ,有些数则不能直接求得,如
,有些数则不能直接求得,如![]() ,但可以通过计算器求. 还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
,但可以通过计算器求. 还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
n | 16 | 0.16 | 0.0016 | 1600 | 160000 | … |
| 4 | 0.4 | 0.04 | 40 | 400 | … |
(1)若![]() ,则
,则![]()
(2)根据你发现的规律,探究下列问题:已知![]() ≈1.435,则:
≈1.435,则:
①![]() ≈ ;
≈ ;
②![]() ≈ ;
≈ ;
(3)根据上述探究过程类比研究一个数的立方根已知![]() ≈1.260,则
≈1.260,则![]() ≈ .
≈ .