题目内容
【题目】如图,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C.
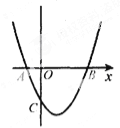
(1)点A的坐标为 点B的坐标为 ,点C的坐标为 ;
(2)设抛物线y=x2-2x-3的顶点坐标为M,求四边形ABMC的面积.
【答案】(1)(-1,0),(3,0),(0,-3);(2)9.
【解析】
试题(1)分别令x=0、y=0即可求出A、B、C的坐标;
(2)运用配方法求出顶点M的坐标,作出抛物线的对称轴,交x轴于点D,则四边形ABMC的面积=△AOC的面积+梯形OCMD的面积+△BDM的面积.
试题解析:(1) 由y=0得x2-2x-3=0.
解得x1=-1,x2=3.
∴点A的坐标(-1,0),点B的坐标(3,0).
由x=0,得y=-3
∴点C的坐标(0,-3)
(2)如图:作出抛物线的对称轴,交x轴于点D,

由y=x2-2x-3=(x-1)2-4得
点M的坐标(1,-4)
四边形ABMC的面积=△AOC的面积+梯形OCMD的面积+△BDM的面积.
=![]()
=9.
考点: 二次函数图象与性质.

练习册系列答案
相关题目