题目内容
1.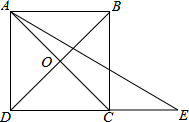 如图,已知正方形ABCD的边长为4,对角线AC与BD相交于点O,点E在DC边的延长线上.若∠CAE=15°,则AE=8.
如图,已知正方形ABCD的边长为4,对角线AC与BD相交于点O,点E在DC边的延长线上.若∠CAE=15°,则AE=8.
分析 先由正方形的性质可得∠BAC=45°,AB∥DC,∠ADC=90°,由∠CAE=15°,根据平行线的性质及角的和差得出∠E=∠BAE=∠BAC-∠CAE=30°.然后在Rt△ADE中,根据30°角所对的直角边等于斜边的一半即可得到AE=2AD=8.
解答 解:∵正方形ABCD的边长为4,对角线AC与BD相交于点O,
∴∠BAC=45°,AB∥DC,∠ADC=90°,
∵∠CAE=15°,
∴∠E=∠BAE=∠BAC-∠CAE=45°-15°=30°.
∵在Rt△ADE中,∠ADE=90°,∠E=30°,
∴AE=2AD=8.
故答案为8.
点评 本题考查了含30度角的直角三角形的性质:在直角三角形中,30°角所对的直角边等于斜边的一半.也考查了正方形的性质,平行线的性质.求出∠E=30°是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
12.一组数据2、3、4、4、5、5、5的中位数和众数分别是( )
| A. | 3.5,5 | B. | 4,4 | C. | 4,5 | D. | 4.5,4 |
9.已知∠A=40°,则它的余角为( )
| A. | 40° | B. | 50° | C. | 130° | D. | 140° |
16.小强和小华两人玩“剪刀、石头、布”游戏,随机出手一次,则两人平局的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
6.函数y=$\frac{{\sqrt{x}}}{2}$中,自变量x的取值范围是( )
| A. | x>0 | B. | x≥0 | C. | x<0 | D. | x≤0 |
13.在△ABC中,AB=12$\sqrt{2}$,AC=13,cos∠B=$\frac{{\sqrt{2}}}{2}$,则BC边长为( )
| A. | 7 | B. | 8 | C. | 8或17 | D. | 7或17 |
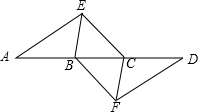 如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.