题目内容
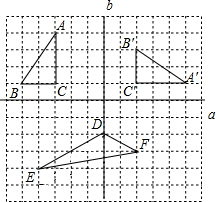
在如图所示的方格图中,每个小正方形的顶点称为“格点”,且 每个小正方形的边长均为1个长度单位,以格点为顶点的图形叫做“格点图形”,根据图形解决下列问题:
每个小正方形的边长均为1个长度单位,以格点为顶点的图形叫做“格点图形”,根据图形解决下列问题:(1)图中格点△A′B′C′是由格点△ABC通过怎样变换得到的?
(2)如图建立直角坐标系后,点A的坐标为(-5,2),点B的坐标为(-5,0),请求出过A点的正比例函数的解析式,并写出图中格点△DEF各顶点的坐标.
分析:(1)根据旋转和平移的图形变换可知.
(2)先设出过A点的正比例函数解析式的一般式,再代入点的坐标即可得出函数解析式.然后从坐标系中读出各点的坐标即可.
(2)先设出过A点的正比例函数解析式的一般式,再代入点的坐标即可得出函数解析式.然后从坐标系中读出各点的坐标即可.
解答:解:(1)格点△A′B′C′是由格点△ABC先绕B点逆时针旋转90°,然后向右平移13个长度单位(或格)得到的.(4分)
(2)设过A点的正比例函数解析式为y=kx,
将A(-5,2)代入上式得,
2=-5k,
k=-
,
∴过A点的正比函数的解析式为y=-
x.(4分)
△DEF各顶点的坐标为:
D(2,-4),E(0,-8),F(7,-7). (3分)
(2)设过A点的正比例函数解析式为y=kx,
将A(-5,2)代入上式得,
2=-5k,
k=-
| 2 |
| 5 |
∴过A点的正比函数的解析式为y=-
| 2 |
| 5 |
△DEF各顶点的坐标为:
D(2,-4),E(0,-8),F(7,-7). (3分)
点评:本题主要考查了旋转变换和平移的性质及求一次函数的解析式的方法.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 23、①在如图所示的方格纸中,按下列要求画图:
23、①在如图所示的方格纸中,按下列要求画图:
 在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”根据图形,解决下面的问题:
在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”根据图形,解决下面的问题: (2008•荔湾区二模)在如图所示的方格图中.根据图形,解决下面的问题:
(2008•荔湾区二模)在如图所示的方格图中.根据图形,解决下面的问题: 为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.