题目内容
 如图,公园里,小颖沿着斜坡AB从A点爬上到B点后,顺着斜坡从B点滑下到C点.已知A、C两点在同一水平线上,∠A=45°,∠C=30°,AB=4米,则BC的长为
如图,公园里,小颖沿着斜坡AB从A点爬上到B点后,顺着斜坡从B点滑下到C点.已知A、C两点在同一水平线上,∠A=45°,∠C=30°,AB=4米,则BC的长为
- A.
 米
米 - B.
 米
米 - C.
 米
米 - D.
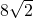 米
米
B
分析:过B点作BD⊥AC于D,根据等腰直角三角形的性质可求BD的长,再根据含30°角的直角三角形的性质可得BC的长.
解答: 解:过B点作BD⊥AC于D.
解:过B点作BD⊥AC于D.
在Rt△ABD中,∵∠A=45°,AB=4米,
∴BD= AB=2
AB=2 米,
米,
在Rt△BCD中,又∵∠C=30°,
∴BC=2BD=4 米.
米.
故选B.
点评:考查了解直角三角形的应用-坡度坡角问题,解题的关键是作出辅助线构造直角三角形,求得AC边上的高BD的长.
分析:过B点作BD⊥AC于D,根据等腰直角三角形的性质可求BD的长,再根据含30°角的直角三角形的性质可得BC的长.
解答:
 解:过B点作BD⊥AC于D.
解:过B点作BD⊥AC于D.在Rt△ABD中,∵∠A=45°,AB=4米,
∴BD=
 AB=2
AB=2 米,
米,在Rt△BCD中,又∵∠C=30°,
∴BC=2BD=4
 米.
米.故选B.
点评:考查了解直角三角形的应用-坡度坡角问题,解题的关键是作出辅助线构造直角三角形,求得AC边上的高BD的长.

练习册系列答案
相关题目
 (2012•宝安区二模)如图,公园里,小颖沿着斜坡AB从A点爬上到B点后,顺着斜坡从B点滑下到C点.已知A、C两点在同一水平线上,∠A=45°,∠C=30°,AB=4米,则BC的长为( )
(2012•宝安区二模)如图,公园里,小颖沿着斜坡AB从A点爬上到B点后,顺着斜坡从B点滑下到C点.已知A、C两点在同一水平线上,∠A=45°,∠C=30°,AB=4米,则BC的长为( )
 米
米 米
米 米
米 米
米
 米
米 米
米 米
米 米
米
 米
米 米
米 米
米 米
米