Question

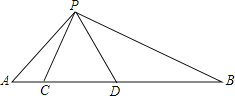
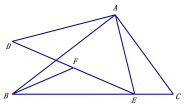
【题目】如图，△ABC∽△ADE，∠BAC =∠ADE =90°，AB=4，AC=3，F是DE的中点，若点E是直线BC上的动点，连接BF，则BF的最小值是_______．

Answer 1

【答案】2

【解析】

连接DB，先求出∠DBE=90°，F是DE的中点，可得BF=DE，再根据当AE⊥BC时，AE最短，此时DE最短，根据直角三角形的面积以及相似三角形的性质，求得DE的最小值，即可得出BF的最小值．

如图，连接DB，

∵∠BAC =90°，AB=4，AC=3，

∴BC=5，

∵△ABC∽△ADE，

∴∠ADE=∠ABC，

又∵∠AOD=∠EOB，

∴△AOD∽△EOB，

∴，

又∵∠AOE=∠DOB，

∴△AOE∽△DOB，

∴∠DBO=∠AEO，

又∵Rt△ADE中,∠ADE+∠AEO=90，又∠ADE=∠ABC，

∴∠DBO +∠ABC =90,即∠DBE=90，

∵F是DE的中点，

∴BF=DE，

∵△ABC∽△ADE，

∴当AE⊥BC时，AE最短，此时DE最短，

当AE⊥BC时,AE= =，

∵△ABC∽△ADE，

∴ ，即3DE= ，

∴DE=4，

∴BF=×4=2.

故答案为：2.