题目内容
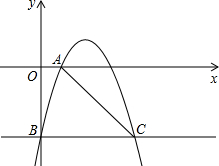 如图,抛物线y=-x2+4x+n经过点A(1,0),与y轴交于点B.过点B且平行于x轴的直线交抛物线于点C.
如图,抛物线y=-x2+4x+n经过点A(1,0),与y轴交于点B.过点B且平行于x轴的直线交抛物线于点C.(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)在该抛物线的对称轴上是否存在点P,使得△ABP的周长最小?若存在,求出P点的坐标;若不存在,请说明理由.
分析:(1)利用待定系数法求解,直接将点A的坐标代入抛物线的解析式中即可.
(2)令(1)的抛物线中,x=0,即可得B点的坐标,B、C关于抛物线对称轴对称,则C点坐标可求,以BC为底、B点纵坐标的绝对值为高,即可求出△ABC的面积.
(3)由于B、C关于抛物线的对称轴对称,所以直线AC与抛物线对称轴的交点即为符合题意的P点,因此联立直线AC的解析式与抛物线对称轴方程即可得解.
(2)令(1)的抛物线中,x=0,即可得B点的坐标,B、C关于抛物线对称轴对称,则C点坐标可求,以BC为底、B点纵坐标的绝对值为高,即可求出△ABC的面积.
(3)由于B、C关于抛物线的对称轴对称,所以直线AC与抛物线对称轴的交点即为符合题意的P点,因此联立直线AC的解析式与抛物线对称轴方程即可得解.
解答:解:(1)将A(1,0)代入y=-x2+4x+n中,得:
-1+4+n=0,解得:n=-3
∴抛物线的解析式:y=-x2+4x-3.
(2)当x=0时,y=-x2+4x-3=-3,所以B(0,-3);
由(1)知,抛物线的对称轴:x=-
=2,
因为BC∥x轴,所以B、C关于对称轴x=2对称,则C(4,-3);
∴S△ABC=
•BC•OB=
×4×3=6.
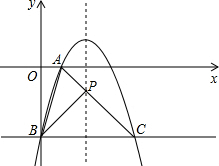 (3)设直线AC的解析式为y=kx+b,代入A(1,0)、C(4,-3),得:
(3)设直线AC的解析式为y=kx+b,代入A(1,0)、C(4,-3),得:
,解得
∴直线AC:y=-x+1;
∵B、C关于抛物线的对称轴对称,
∴点P为直线AC与抛物线对称轴x=2的交点,依题意,有:
,解得
∴P(2,-1).
-1+4+n=0,解得:n=-3
∴抛物线的解析式:y=-x2+4x-3.
(2)当x=0时,y=-x2+4x-3=-3,所以B(0,-3);
由(1)知,抛物线的对称轴:x=-
| b |
| 2a |
因为BC∥x轴,所以B、C关于对称轴x=2对称,则C(4,-3);
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
 (3)设直线AC的解析式为y=kx+b,代入A(1,0)、C(4,-3),得:
(3)设直线AC的解析式为y=kx+b,代入A(1,0)、C(4,-3),得:
|
|
∴直线AC:y=-x+1;
∵B、C关于抛物线的对称轴对称,
∴点P为直线AC与抛物线对称轴x=2的交点,依题意,有:
|
|
∴P(2,-1).
点评:此题考查的内容较为简单,主要涉及:二次函数解析式的确定、三角形面积的求法以及轴对称图形的性质;(3)题中,充分理解轴对称图形的性质以及两点之间线段最短是解答题目的关键,该类型题在二次函数综合题中经常出现,需要牢固掌握.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 如图,抛物线y=ax2+bx+c(a≠0)与x轴两交点是A(-1,0),B(3,0),则如图可知y<0时,x的取值范围是( )
如图,抛物线y=ax2+bx+c(a≠0)与x轴两交点是A(-1,0),B(3,0),则如图可知y<0时,x的取值范围是( )| A、-1<x<3 | B、3<x<-1 | C、x>-1或x<3 | D、x<-1或x>3 |
 26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG|
26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG| 如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4).
如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4). 以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由.
以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由. .点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于D点.
.点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于D点.