题目内容
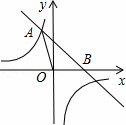
如图,已知直线y=﹣x+4与反比例函数![]() 的图象相交于点A(﹣2,a),并且与x轴相交于点B.
的图象相交于点A(﹣2,a),并且与x轴相交于点B.
(1)求a的值;
(2)求反比例函数的表达式;
(3)求△AOB的面积.
考点:
反比例函数综合题.
专题:
待定系数法.
分析:
(1)把A的坐标代入直线解析式求a;
(2)把求出的A点坐标代入反比例解析式中求k,从而得解析式;求B点坐标,结合A点坐标求面积.
解答:
解:(1)将A(﹣2,a)代入y=﹣x+4中,得:a=﹣(﹣2)+4,所以a=6(2)由(1)得:A(﹣2,6)
将A(﹣2,6)代入![]() 中,得到:
中,得到:![]() ,即k=﹣12
,即k=﹣12
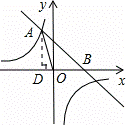
所以反比例函数的表达式为:![]() (3)如图:过A点作AD⊥x轴于D;
(3)如图:过A点作AD⊥x轴于D;
∵A(﹣2,6)
∴AD=6
在直线y=﹣x+4中,令y=0,得x=4
∴B(4,0),即OB=4
∴△AOB的面积S=![]() OB×AD=
OB×AD=![]() ×4×6=12.
×4×6=12.
点评:
熟练掌握解析式的求法.在进行与线段有关的计算时,注意点的坐标与线段长度的关系.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.
16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE. 5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( )
5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( ) 如图,已知直线l1:
如图,已知直线l1: (2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2=
(2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2= 如图,已知直线m∥n,则下列结论成立的是( )
如图,已知直线m∥n,则下列结论成立的是( )