Question

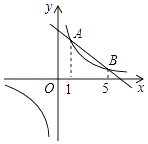
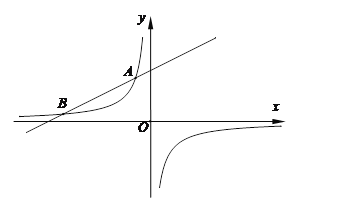
【题目】如图，反比例函数与一次函数的图象交于点A（－2，6）、点B（，1）.

（1）求反比例函数与一次函数的表达式；

（2）点E为y轴上一个动点，若S△AEB=5，求点E的坐标．

（3）将一次函数的图象沿轴向下平移n个单位，使平移后的图象与反比例函数的图象有且只有一个交点，求n的值.

Answer 1

【答案】（1），（2）（0，6）或（0，8）（3）或

【解析】（1）利用待定系数法求两函数的解析式；

（2）设点E的坐标为（0，m），连接AE，BE，先求出点P的坐标（0，7），得出PE=|m-7|，根据S△AEB=S△BEP-S△AEP=5，求出m的值，从而得出点E的坐标；

（3）设平移后的一次函数的解析式为y=，由=由题意，△=0，解方程即可.

（1）把点A（－2，6）代入反比例函数y=中，

得：k=-2×6=-12，

∴反比例函数解析式为：，

当y=1时, n=-12，

∴B(-12,1)，

则，

解得：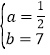

∴一次函数的解析式为：y=x+7；

（2）设于y轴的交点为P，易得P（0,7）,设E（0,m）

由题意，PE=|m7|.

则S△AEB= S△BEP－S△AEP，

得，

∴m1=6，m2=8．

∴点E的坐标为（0，6）或（0，8）．

（3）由题意得=

方程变形为

解得或