Question

【题目】如图，扇形DOE的半径为3，边长为 的菱形OABC的顶点A，C，B分别在OD，OE， 上，若把扇形DOE围成一个圆锥，则此圆锥的高为（ ）
A.
B.
C.
D.

Answer 1

【答案】D
【解析】解：连接OB，AC，BO与AC相交于点F，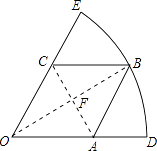
∵在菱形OABC中，AC⊥BO，CF=AF，FO=BF，∠COB=∠BOA，
又∵扇形DOE的半径为3，
∴FO=BF=1.5，
∵菱形OABC的边长为 ，
cos∠FOC= = = ，
∴∠FOC=30°，
∴∠EOD=2×30°=60°，
∴ = =π，
底面圆的周长为：2πr=π，
解得：r= ，圆锥母线为：3，
则此圆锥的高为： = ，
故选：D．
连接OB，AC，BO与AC相交于点F，首先利用菱形的性质以及利用三角函数关系得出∠FOC=30°，进而得出底面圆锥的周长，即可得出底面圆的半径和母线长，利用勾股定理得出圆锥的高即可．