题目内容
如图，点D是△ABC的边BC的中点，点E是AD的中点，若S△BDE=1，则SABC=考点：三角形的面积
专题：
分析：根据△ABE和△BDE底和高相等即可求得其面积相等，同理可证△AEC和△DEC面积相等，再根据BD=CD可以求得△BDE和△CDE面积相等，即可求得△ABC的面积．
解答：解：∵点E是AD的中点，
∴AE=BE，
∴△ABE和△BDE面积相等，
△AEC和△DEC面积相等，
∵D是BC中点，∴BD=CD，
∴△BDE和△CDE面积相等，
∴△ABC的面积=4×△BDE的面积=4，
故答案为4．
∴AE=BE，
∴△ABE和△BDE面积相等，
△AEC和△DEC面积相等，
∵D是BC中点，∴BD=CD，
∴△BDE和△CDE面积相等，
∴△ABC的面积=4×△BDE的面积=4，
故答案为4．
点评：本题考查了三角形面积的计算，本题中根据两个三角形底和高相等则其面积相等解题是解题的关键．
练习册系列答案
相关题目
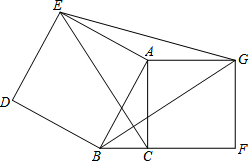如图，在△ABC中，∠ACB=90°，分别以边AB、AC向外作正方形ABDE和正方形ACFG，连接CE，BG，EG．（正方形的各边都相等，各角均为90°）
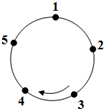（1）如图，圆上有五个点，这五个点将圆分成五等份（每一份称为一段弧长），把这五
作图题：已知平面上四个点A，B，C，D，如图：