题目内容
若P是边长为2的等边三角形内任一点,则P到这个三角形三边的距离之和是
- A.1
- B.

- C.2
- D.

B
分析:先画图,再根据图可得出S△ABC=S△PAB+S△PBC+S△PAC,再利用三角形的面积公式可得h=PE+PF+PD,而等边三角形底边上的高等于边长乘以sin60°,从而易求PE+PF+PD= .
.
解答: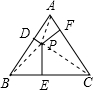 解:如右图所示,
解:如右图所示,
P是等边三角形ABC内一点,PD、PE、PF分别是点P到AB、BC、AB三边的垂线段,
连接PA、PB、PC,设此三角形BC边上的高是h,
∵S△ABC=S△PAB+S△PBC+S△PAC,
∴ BC•h=
BC•h= BC•PE+
BC•PE+ AC•PF+
AC•PF+ AB•PD,
AB•PD,
∵△ABC是等边三角形,
∴AB=BC=AC=2,
∴h=PE+PF+PD,
又∵等边三角形地边上的高h=边长×sin60°=2× =
= ,
,
∴PE+PF+PD= .
.
故选B.
点评:本题考查了等边三角形的性质、三角形的面积、特殊三角函数值.解题的关键是能从图中看出三个小三角形的面积和等于大三角形的面积,据此作答.
分析:先画图,再根据图可得出S△ABC=S△PAB+S△PBC+S△PAC,再利用三角形的面积公式可得h=PE+PF+PD,而等边三角形底边上的高等于边长乘以sin60°,从而易求PE+PF+PD=
 .
.解答:
 解:如右图所示,
解:如右图所示,P是等边三角形ABC内一点,PD、PE、PF分别是点P到AB、BC、AB三边的垂线段,
连接PA、PB、PC,设此三角形BC边上的高是h,
∵S△ABC=S△PAB+S△PBC+S△PAC,
∴
 BC•h=
BC•h= BC•PE+
BC•PE+ AC•PF+
AC•PF+ AB•PD,
AB•PD,∵△ABC是等边三角形,
∴AB=BC=AC=2,
∴h=PE+PF+PD,
又∵等边三角形地边上的高h=边长×sin60°=2×
 =
= ,
,∴PE+PF+PD=
 .
.故选B.
点评:本题考查了等边三角形的性质、三角形的面积、特殊三角函数值.解题的关键是能从图中看出三个小三角形的面积和等于大三角形的面积,据此作答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
正方形ABCD中,E、F两点分别是BC、CD上的点.若△AEF是边长为
的等边三角形,则正方形ABCD的边长为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
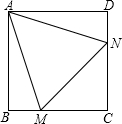 如图,在正方形ABCD中,M、N两点分别是BC、CD边上的点,若△AMN是边长为
如图,在正方形ABCD中,M、N两点分别是BC、CD边上的点,若△AMN是边长为