题目内容
设a+b+c+3=2（
），则a2+b2+c2=________．
5
分析：先将a+b+c+3=2（）变形配方，再利用非负数的性质求出a，b，c的值，代入计算即可．
解答：∵a+b+c+3=2（），
∴a-2
+1+[（b+1）-2
+1]+[（c-1）-2
+1]=0，
∴（
）2+（-1）2+（-1）2=0，
∴a=1，b=0，c=2，
∴a2+b2+c2=5．
故答案为5．
点评：本题考查了配方法的应用：配方法的理论依据是公式a2±2ab+b2=（a±b）2，配方法的关键是：先将一元二次方程的二次项系数化为1，然后在方程两边同时加上一次项系数一半的平方．
分析：先将a+b+c+3=2（
）变形配方，再利用非负数的性质求出a，b，c的值，代入计算即可．解答：∵a+b+c+3=2（
），∴a-2
+1+[（b+1）-2+1]+[（c-1）-2+1]=0，∴（
）2+（-1）2+（-1）2=0，∴a=1，b=0，c=2，
∴a2+b2+c2=5．
故答案为5．
点评：本题考查了配方法的应用：配方法的理论依据是公式a2±2ab+b2=（a±b）2，配方法的关键是：先将一元二次方程的二次项系数化为1，然后在方程两边同时加上一次项系数一半的平方．
练习册系列答案
相关题目
八年级某班级部分同学去植树，若每人平均植树7棵，还剩9棵，若每人平均植树9棵，则有1名同学植树的棵数不到8棵．若设同学人数为x人，下列各项能准确的求出同学人数与种植的树木的数量的是（ ）
| A、7x+9-9（x-1）＞0 | |||||
| B、7x+9-9（x-1）＜8 | |||||
C、
| |||||
D、
|
已知⊙O1的半径为R，周长为C．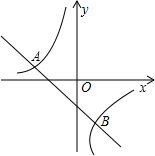
如图，若反比例函数y=-