题目内容
如图:已知△ABC中,AB=5,BC=3,AC=4,PQ∥AB,P点在AC上(与A、C不重合),Q在BC上.(1)当△PQC的面积与四边形PABQ的面积相等时,求CP的长;
(2)当△PQC的周长与四边形PABQ的周长相等时,求CP的长;
(3)试问:在AB上是否存在一点M,使得△PQM为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出PQ的长.

【答案】分析:(1)由于PQ∥AB,故△PQC∽△ABC,当△PQC的面积与四边形PABQ的面积相等时,△CPQ与△CAB的面积比为1:2,根据相似三角形的面积比等于相似比的平方,可求出CP的长;
(2)由于△PQC∽△ABC,根据相似三角形的性质,可用CP表示出PQ和CQ的长,进而可表示出AP、BQ的长.根据△CPQ和四边形ABQP的周长相等,可将相关的各边相加,即可求出CP的长;
(3)因为不能确定哪个角是直角,故应分类讨论.
①当∠MPQ=90°,且PM=PQ时.因为△CPQ∽△CAB,根据相似三角形边长的比等于高的比,可求出PQ的值;
②∠PQM=90°时与①相同;
③当∠PMQ=90°,且PM=MQ时,过M作ME⊥PQ,则ME= PQ,根据相似三角形边长的比等于高的比,可求出PQ的值.
PQ,根据相似三角形边长的比等于高的比,可求出PQ的值.
解答:解:(1)∵PQ∥AB,
∴△PQC∽△ABC,
∵S△PQC=S四边形PABQ,
∴S△PQC:S△ABC=1:2,
∴ =
= =
= ,
,
∴CP= •CA=2
•CA=2 ;
;
(2)∵△PQC∽△ABC,
∴ =
= =
= ,
,
∴ =
= ,
,
∴CQ= CP,
CP,
同理:PQ= CP,
CP,
∴l△PCQ=CP+PQ+CQ=CP+ CP+
CP+ CP=3CP,
CP=3CP,
I四边形PABQ=PA+AB+BQ+PQ,
=4-CP+AB+3-CQ+PQ
=4-CP+5+3- CP+
CP+ CP
CP
=12- CP,
CP,
∴12- CP=3CP
CP=3CP
∴ CP=12
CP=12
∴CP= ;
;
(3)∵AC=4,AB=5,BC=3
∴△ABC中AB边上的高为
①当∠MPQ=90°,且PM=PQ时,
∵△CPQ∽△CAB
∴ =
=

∴ =
=
∴PQ=
②当∠PQM=90°时与①相同
③当∠PMQ=90°,且PM=MQ时
过M作ME⊥PQ
则ME= PQ
PQ
∴△CPQ的高为 -ME=
-ME= -
- PQ
PQ
∴ =
=
∴ =
=
∴PQ= .
.
综合①②③可知:点M存在,PQ的长为 或
或 .
.
点评:本题比较复杂,综合考查了相似三角形及直角三角形的性质,难度较大.
(2)由于△PQC∽△ABC,根据相似三角形的性质,可用CP表示出PQ和CQ的长,进而可表示出AP、BQ的长.根据△CPQ和四边形ABQP的周长相等,可将相关的各边相加,即可求出CP的长;
(3)因为不能确定哪个角是直角,故应分类讨论.
①当∠MPQ=90°,且PM=PQ时.因为△CPQ∽△CAB,根据相似三角形边长的比等于高的比,可求出PQ的值;
②∠PQM=90°时与①相同;
③当∠PMQ=90°,且PM=MQ时,过M作ME⊥PQ,则ME=
 PQ,根据相似三角形边长的比等于高的比,可求出PQ的值.
PQ,根据相似三角形边长的比等于高的比,可求出PQ的值.解答:解:(1)∵PQ∥AB,
∴△PQC∽△ABC,
∵S△PQC=S四边形PABQ,
∴S△PQC:S△ABC=1:2,
∴
 =
= =
= ,
,∴CP=
 •CA=2
•CA=2 ;
;(2)∵△PQC∽△ABC,
∴
 =
= =
= ,
,∴
 =
= ,
,∴CQ=
 CP,
CP,同理:PQ=
 CP,
CP,∴l△PCQ=CP+PQ+CQ=CP+
 CP+
CP+ CP=3CP,
CP=3CP,I四边形PABQ=PA+AB+BQ+PQ,
=4-CP+AB+3-CQ+PQ
=4-CP+5+3-
 CP+
CP+ CP
CP=12-
 CP,
CP,∴12-
 CP=3CP
CP=3CP∴
 CP=12
CP=12∴CP=
 ;
;(3)∵AC=4,AB=5,BC=3
∴△ABC中AB边上的高为

①当∠MPQ=90°,且PM=PQ时,
∵△CPQ∽△CAB
∴
 =
=

∴
 =
=
∴PQ=

②当∠PQM=90°时与①相同
③当∠PMQ=90°,且PM=MQ时
过M作ME⊥PQ

则ME=
 PQ
PQ∴△CPQ的高为
 -ME=
-ME= -
- PQ
PQ∴
 =
=
∴
 =
=
∴PQ=
 .
.综合①②③可知:点M存在,PQ的长为
 或
或 .
.点评:本题比较复杂,综合考查了相似三角形及直角三角形的性质,难度较大.

练习册系列答案
相关题目
 如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF.
如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF.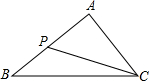 如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( )
如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( ) (2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( )
(2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( ) 如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( )
如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( ) 如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )
如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )