题目内容
(2012•昌平区二模)类比学习:
有这样一个命题:设x、y、z都是小于1的正数,求证:x(1-y)+y(1-z)+z(1-x)<1.
小明同学是这样证明的:如图,作边长为1的正三角形ABC,并分别在其边上截取AD=x,BE=z,CF=y,设△ADF、△CEF和△BDE的面积分别为S1、S2、S3,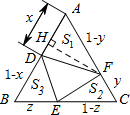
则S1=
x(1-y)sin60°,
S2=
y(1-z)sin60°,
S3=
z(1-x)sin60°.
由 S1+S2+S3<S△ABC,得
x(1-y)sin60°+
y(1-z)sin60°+
z(1-x)sin60°<
.
所以 x(1-y)+y(1-z)+z(1-x)<1.
类比实践:
已知正数a、b、c、d,x、y、z、t满足a+x=b+y=c+z=d+t=k.
求证:ay+bz+ct+dx<2k2.
有这样一个命题:设x、y、z都是小于1的正数,求证:x(1-y)+y(1-z)+z(1-x)<1.
小明同学是这样证明的:如图,作边长为1的正三角形ABC,并分别在其边上截取AD=x,BE=z,CF=y,设△ADF、△CEF和△BDE的面积分别为S1、S2、S3,

则S1=
| 1 |
| 2 |
S2=
| 1 |
| 2 |
S3=
| 1 |
| 2 |
由 S1+S2+S3<S△ABC,得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
所以 x(1-y)+y(1-z)+z(1-x)<1.
类比实践:
已知正数a、b、c、d,x、y、z、t满足a+x=b+y=c+z=d+t=k.
求证:ay+bz+ct+dx<2k2.
分析:首先作出边长为k的正方形ABCD,并分别在各边上截取:AE=a,DH=b,CG=c,BF=d,则BE=x,AH=y,DG=z,CF=t,利用图形面积求出
ay+
dx+
ct+
bz<k2,进而得出答案即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 证明:如图,作边长为k的正方形ABCD.
证明:如图,作边长为k的正方形ABCD.
并分别在各边上截取:
AE=a,DH=b,CG=c,BF=d,
∵a+x=b+y=c+z=d+t=k,
∴BE=x,AH=y,DG=z,CF=t.
∵∠A=∠B=∠C=∠D=90°,
∴S1=
ay,S2=
dx,S3=
ct,S4=
bz.
∵S1+S2+S3+S4<S正方形ABCD,
∴
ay+
dx+
ct+
bz<k2.
∴ay+bz+ct+dx<2k2.
 证明:如图,作边长为k的正方形ABCD.
证明:如图,作边长为k的正方形ABCD.并分别在各边上截取:
AE=a,DH=b,CG=c,BF=d,
∵a+x=b+y=c+z=d+t=k,
∴BE=x,AH=y,DG=z,CF=t.
∵∠A=∠B=∠C=∠D=90°,
∴S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵S1+S2+S3+S4<S正方形ABCD,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴ay+bz+ct+dx<2k2.
点评:此题主要考查了正方形的性质,根据已知构造正方形进而表示出各三角形面积是解题关键.

练习册系列答案
相关题目
 (2012•昌平区二模)如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠ABC=70°,则∠BDC的度数为( )
(2012•昌平区二模)如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠ABC=70°,则∠BDC的度数为( )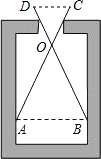 (2012•昌平区二模)如图,用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC:OA=1:2,量得CD=10,则零件的内孔直径AB长为( )
(2012•昌平区二模)如图,用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC:OA=1:2,量得CD=10,则零件的内孔直径AB长为( ) (2012•昌平区二模)如图的方格纸中,每个小方格都是边长为1的正方形,A、B两点是方格纸中的两个格点,在4×5的方格纸中,找出格点C,使△ABC的面积为1个平方单位,则满足条件的格点C的个数是
(2012•昌平区二模)如图的方格纸中,每个小方格都是边长为1的正方形,A、B两点是方格纸中的两个格点,在4×5的方格纸中,找出格点C,使△ABC的面积为1个平方单位,则满足条件的格点C的个数是