题目内容
【题目】在平面直角坐标系xOy中,点P,Q(两点可以重合)在x轴上,点P的横坐标为m,点Q的横坐标为n,若平面内的点M的坐标为(n,|m﹣n|),则称点M为P,Q的跟随点.
(1)若m=0,
①当n=3时,P,Q的跟随点的坐标为 ;
②写出P,Q的跟随点的坐标;(用含n的式子表示);
③记函数y=kx﹣1(﹣1≤x≤1,k≠0)的图象为图形G,若图形G上不存在P,Q的跟随点,求k的取值范围;
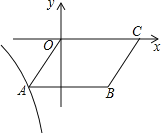
(2)⊙A的圆心为A(0,2),半径为1,若⊙A上存在P,Q的跟随点,直接写出m的取值范围.
【答案】(1)①(3,3);②(n,n)或(n,﹣n);③﹣2<k<0或0<k<2;(2)﹣2![]() m
m![]() 2或2
2或2![]() m≤2
m≤2![]()
【解析】
(1)①将m和n的值代入点M的坐标表达式中计算即可;
②将![]() 代入点M的坐标表达式,再分
代入点M的坐标表达式,再分![]() 和
和![]() 两种情况,去绝对值即可得;
两种情况,去绝对值即可得;
③根据②得出点M所在的函数图象,再画出图象,分![]() 和
和![]() 两种情况讨论,分别建立不等式求解即可;
两种情况讨论,分别建立不等式求解即可;
(2)先由跟随点的定义得出点M在![]() 的图象上,再根据直线与圆的位置关系确认符合题意的临界值,然后利用三角函数值、线段的距离求解即可.
的图象上,再根据直线与圆的位置关系确认符合题意的临界值,然后利用三角函数值、线段的距离求解即可.
(1)①把![]() 代入点P,Q的跟随点M的坐标
代入点P,Q的跟随点M的坐标![]()
故答案为:![]() ;
;
②把![]() 代入P,Q的跟随点M的坐标
代入P,Q的跟随点M的坐标![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
所以P,Q的跟随点的坐标为![]() 或
或![]() ;
;
③由②可知,当![]() 时,P,Q的跟随点在函数
时,P,Q的跟随点在函数![]() 或
或![]() 的图象上
的图象上
由题意,需分![]() 和
和![]() 两种情况:
两种情况:
当![]() 时,如图,要使图形G上不存在P,Q的跟随点,则在
时,如图,要使图形G上不存在P,Q的跟随点,则在![]() 处,
处,![]() 的函数值需小于
的函数值需小于![]() 的函数值,即
的函数值,即![]() ,解得
,解得![]()
故此时k的取值范围为![]()
当![]() 时,如图,要使图形G上不存在P,Q的跟随点,则在
时,如图,要使图形G上不存在P,Q的跟随点,则在![]() 处,
处,![]() 的函数值需小于
的函数值需小于![]() 的函数值,即
的函数值,即![]() ,解得
,解得![]()
故此时k的取值范围为![]()
综上,k的取值范围为![]() 或
或![]() ;
;
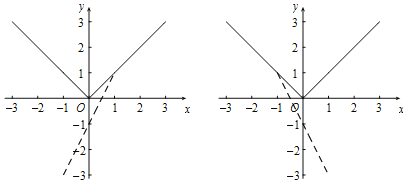
(2)由跟随点的定义可知,点M在![]() 的图象上,即点M在
的图象上,即点M在![]() 或
或![]() 的图象上
的图象上
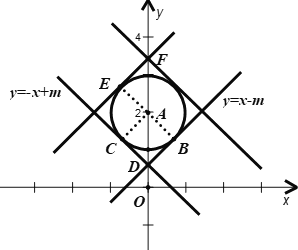
如图,当直线与圆A相切时,是符合要求的临界位置
当点M在![]() 的图象上时,直线与y轴的交点坐标为
的图象上时,直线与y轴的交点坐标为![]()
由直线的解析式和圆的切线性质得:![]()
则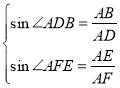 ,即
,即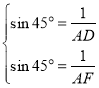 ,解得
,解得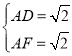
![]() 点A坐标为
点A坐标为![]()
![]() ,解得
,解得![]()
![]() ,解得
,解得![]()
故此时m的取值范围为![]()
同理可得:当点M在![]() 图象上时,m的取值范围为
图象上时,m的取值范围为![]()
综上,m的取值范围为![]() 或
或![]() .
.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案【题目】某厂接到一批订单,按要求要20天内完成,每件产品的出厂价为40元,每件产品的生产成本m元与时间x天(x为整数)之间的一次函数关系如下表:
天数(x) | 1 | 4 | 6 | … |
每件成本(m) | 23 | 20 | 18 | … |
小张每天生产的件数y件与x天(x为整数)之间满足如下关系为:![]() .
.
(1)求m与x之间的函数关系式;
(2)若第x天的利润为W元,求W与x之间的函数关系式,并求出小张在哪天利润最大,最大利润是多少元;
(3)在生产的前10天中,公司决定每件产品捐赠a元(a<7)给公益事业,调查发现,扣除捐赠后的日销售利润随x增大而增大,直接写出a的取值范围.