题目内容
如图所示,矩形ABCD,AB>AD,E在AD上,将△ABE沿BE折叠后,A点正好落在CD上的点F。
【小题1】(1)用尺规作出E、F;
【小题2】(2)若AE=5,DE=3,求折痕BE的长;
【小题3】(3)试判断四边形ABFE是否一定有内切圆。
【小题1】解:(1
 )作法:①作BF=BA交CD于F。
)作法:①作BF=BA交CD于F。②连BF作∠ABF的平分线,则点E、F为所求。

【小题2】(2)连接EF
由条件知:Rt△ABE≌Rt△FBE
∴EF=AE
又AE=5,DE=3,∠D=90°

又BE⊥A
 F
F∴Rt△ADF∽Rt△BAE



【小题3】(3)假设四边形ABFE有内切圆,则圆心必在BE上。

设圆心为点I,内切圆半径为r,则有


∴此四边形ABFE一定有内切圆解析:
略

练习册系列答案
相关题目
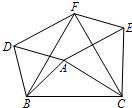 18、如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.
18、如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.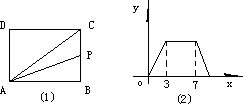
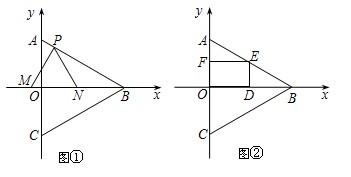
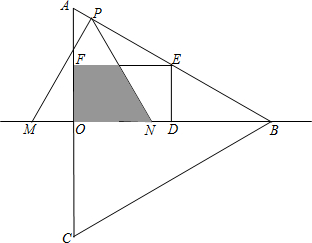 边在△AOB内部作如图所示的矩形ODEF,点E在线段AB上.
边在△AOB内部作如图所示的矩形ODEF,点E在线段AB上. (2012•邵阳)如图所示,在△ABC中,AB=AC,∠A<90°,边BC、CA、AB的中点分别是D、E、F,则四边形AFDE是( )
(2012•邵阳)如图所示,在△ABC中,AB=AC,∠A<90°,边BC、CA、AB的中点分别是D、E、F,则四边形AFDE是( )