题目内容
如图,∠ABM为直角,点C为线段BA的中点,点D是射线BM上的一个动点(不与点B重合)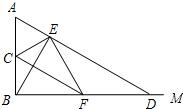 ,连接AD,作BE⊥AD,垂足为E,连接CE,过点E作EF⊥CE,交BD于F.
,连接AD,作BE⊥AD,垂足为E,连接CE,过点E作EF⊥CE,交BD于F.(1)求证:BF=FD;
(2)点D在运动过程中能否使得四边形ACFE为平行四边形?如不能,请说明理由;如能,求出此时∠A的度数.
分析:(1)欲证BF=FD,可证BF=EF,FD=EF.欲证BF=EF,在△BEF中,可证∠BEF=∠EBF,由于CE为直角△ABE斜边AB的中线,所以CB=CE,根据等边对等角,得出∠CEB=∠CBE,又∠CEF=∠CBF=90°,由等角的余角相等得出∠BEF=∠EBF;欲证FD=EF,在△FED中,可证∠FED=∠EDF,由于∠BEF+∠FED=90°,∠EBD+∠EDB=90°,而∠BEF=∠EBF,故∠FED=∠EDF.
(2)假设点D在运动过程中能使四边形ACFE为平行四边形,则AC∥EF,AC=EF,由(1)知AC=CB=
AB,EF=BF=
BD,则BC=EF=BF,即BA=BD,∠A=45°.
(2)假设点D在运动过程中能使四边形ACFE为平行四边形,则AC∥EF,AC=EF,由(1)知AC=CB=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)在Rt△AEB中,∵AC=BC,
∴CE=
AB,
∴CB=CE,
∴∠CEB=∠CBE.
∵∠CEF=∠CBF=90°,
∴∠BEF=∠EBF,
∴EF=BF.
∵∠BEF+∠FED=90°,∠EBD+∠EDB=90°,
∴∠FED=∠EDF,
∵EF=FD.
∴BF=FD.
(2)能.理由如下:
若四边形ACFE为平行四边形,则AC∥EF,AC=EF,
∴BC=BF,
∴BA=BD,∠A=45°.
∴当∠A=45°时四边形ACFE为平行四边形.
∴CE=
| 1 |
| 2 |
∴CB=CE,
∴∠CEB=∠CBE.
∵∠CEF=∠CBF=90°,
∴∠BEF=∠EBF,
∴EF=BF.
∵∠BEF+∠FED=90°,∠EBD+∠EDB=90°,
∴∠FED=∠EDF,
∵EF=FD.
∴BF=FD.
(2)能.理由如下:
若四边形ACFE为平行四边形,则AC∥EF,AC=EF,
∴BC=BF,
∴BA=BD,∠A=45°.
∴当∠A=45°时四边形ACFE为平行四边形.
点评:本题考查了平行四边形的判定,在应用判定定理判定平行四边形时,应仔细观察题目所给的条件,仔细选择适合于题目的判定方法进行解答,避免混用判定方法.

练习册系列答案
相关题目
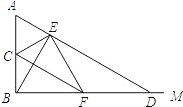 ,连接AD,作BE⊥AD,垂足为E,连接CE,过点E作EF⊥CE,交BD于F.
,连接AD,作BE⊥AD,垂足为E,连接CE,过点E作EF⊥CE,交BD于F.

 DA,并说明理由.
DA,并说明理由.