题目内容
已知矩形面积为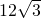 cm2,两条对角线所成的锐角为60°,那么这个矩形中较短的一条边长是________cm.
cm2,两条对角线所成的锐角为60°,那么这个矩形中较短的一条边长是________cm.
2
分析:根据矩形性质得出AO=CO=BO=DO,进而得出AB=BO,再利用勾股定理求出AB,AC,即可得出答案.
解答: 解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,
∴AO=CO=BO=DO,
∵∠AOB=60°,
∴△ABO是等边三角形,
∴AB=BO,∠BAC=60°,
∴∠BCA=30°,
设AB=xcm,则AC=2xcm,
∴BC= =
= xcm,
xcm,
∵矩形面积为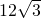 cm2,
cm2,
∴AB•BC=x• x=12
x=12 ,
,
x=2 cm.
cm.
故答案为:2 .
.
点评:此题主要考查了矩形的性质和等边三角形的性质与判定以及勾股定理的应用,根据已知用同一未知数表示出AB,AC,BC的长是解决问题的关键.

分析:根据矩形性质得出AO=CO=BO=DO,进而得出AB=BO,再利用勾股定理求出AB,AC,即可得出答案.
解答:
 解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,∴AO=CO=BO=DO,
∵∠AOB=60°,
∴△ABO是等边三角形,
∴AB=BO,∠BAC=60°,
∴∠BCA=30°,
设AB=xcm,则AC=2xcm,
∴BC=
 =
= xcm,
xcm,∵矩形面积为
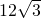 cm2,
cm2,∴AB•BC=x•
 x=12
x=12 ,
,x=2
 cm.
cm.故答案为:2
 .
.点评:此题主要考查了矩形的性质和等边三角形的性质与判定以及勾股定理的应用,根据已知用同一未知数表示出AB,AC,BC的长是解决问题的关键.

练习册系列答案
相关题目