Question

【题目】如图，平面直角坐标系中，直线经过点、，点是第一象限的点且，过点作轴，垂足为，．

（1）求直线的解析式和点的坐标；

（2）试说明：；

（3）若点是直线上的一个动点，在轴上存在另一个点，且以、、、为顶点的四边形是平行四边形，请直接写出点的坐标．

Answer 1

【答案】（1），；（2）详见解析；（3），，

【解析】

（1）将A、B坐标代入可得直线解析式，设B（1，m），由得1+m2=5，解之可得答案；
（2）利用边角边证明△AOD与△OCB全等，从而得到∠OAD=∠COB，根据∠COB+∠AOB=90°可得∠OAD+∠AOB=90°，从而得到∠AEO=90°，得证；
（3）根据平行四边形的对边平行且相等可得BM∥AN且BM=AN，令y=2求出点M的坐标，从而得到BM的长度，再分点N在点O的左边与右边、点N关于A的对称点三种情况讨论求出点N的坐标．

解：（1）把，代入

得解得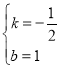

∴解析式为

∵，轴

设

∵，

∴，（负值舍去）

∴；

（2）∵，，，

∴，

∵

∴

∴

∵

∴

∴∠AEO=90°，

∴；

（3）∵点N在x轴上，O、B、M、N为顶点的四边形是平行四边形，
∴BM∥x轴，且BM=ON，
根据（1），点B的坐标为（1，2），
∴-x+1=2，
解得x=-2，
∴点M的坐标为（-2，2），
∴BM=1-（-2）=1+2=3，
①点N在点O的左边时，ON=BM=3，
∴点N的坐标为（-3，0），
②点N在点O的右边时，ON=BM=3，
∴点N的坐标为（3，0），
③作N（-3，0）关于A对称的点N′，则N′也符合，
点N′的坐标是（7，0），
综上所述，点N的坐标为（-3，0）或（3，0）或（7，0）．