题目内容
已知：如图，以△ABC的BC边为直径的半圆交AB于D，交AC于E，过E点作EF⊥BC，垂足为F，且BF：FC=5：1，AB=8，AE=2．求EC的长．
分析：连接BE，所求线段EC就成为了一个直角三角形BCE的直角边，可根据勾股定理来求解，而BE能通过Rt△ABE利用勾股定理求出，BC则需要通过△BEF∽△BCE及BF：FC=5：1来求解．
解答：
解：连接BE，则BE⊥AC．
∴BE2=AB2-AE2=82-22=60．
设FC=x，则BF=5x，BC=6x．
∵∠EFB=∠CEB，∠EBF=∠CBE，
∴△BEF∽△BCE，
∴
=
，
∴BE2=BF•BC．
即60=5x•6x，
∵FC=x＞0，
∴x=
，
∴BC=6
．
∵EC2=BC2-BE2=12，
∴EC=2
．
解：连接BE，则BE⊥AC．∴BE2=AB2-AE2=82-22=60．
设FC=x，则BF=5x，BC=6x．
∵∠EFB=∠CEB，∠EBF=∠CBE，
∴△BEF∽△BCE，
∴
| BF |
| BE |
| BE |
| BC |
∴BE2=BF•BC．
即60=5x•6x，
∵FC=x＞0，
∴x=
| 2 |
∴BC=6
| 2 |
∵EC2=BC2-BE2=12，
∴EC=2
| 3 |
点评：此题考查了相似三角形的判定方法，勾股定理及圆周角定理等知识点的综合运用．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
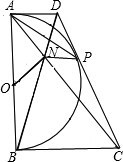已知：如图，以定线段AB为直径作半圆O，P为半圆上任意一点（异于A，B），过点P作半圆O的切线分别交过A，B两点的切线于D，C，AC、BD相交于N点，连接ON、NP．下列结论：①四边形ANPD是梯形；②ON=NP；③DP•PC为定值；④PA为∠NPD的平分线．其中一定成立的是（ ）
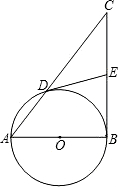已知：如图，以△ABC的边AB为直径的⊙O交边AC于点D，且过点D的切线DE平分边BC．
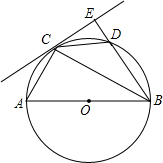已知：如图，以Rt△ABC的斜边AB为直径作⊙O，D是⊙O上的点，且有AC=CD．过点C作⊙O的切线，与BD的延长线交于点E，连接CD．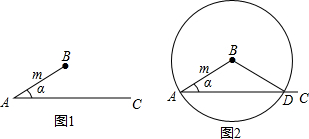
已知：如图，以△ABC的一边BC为直径作半圆，交AB于E，过E点作半圆O的切线恰与AC垂直，试确定边BC与AC的大小关系，并证明你的结论．