题目内容
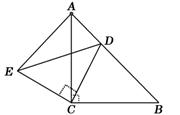
如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,
求证:(1)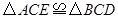 ;(2)
;(2)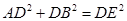 .
.
【答案】
(1)△ACE≌△BCD;(2)AD2+DB2=DE2.
【解析】
试题分析:
试题解析:证明:(1)∵△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,
∴EC=CD,AC=CB,
∠ACB﹣∠ACD=∠ECD﹣∠ACD.
∴∠ACE=∠BCD.
∴△ACE≌△BCD.
(2)∵△ACB是等腰直角三角形,
∴∠B=∠BAC=45°.
∵△ACE≌△BCD,
∴∠B=∠CAE=45°
∴∠DAE=∠CAE+∠BAC=45°+45°=90°,
∴AD2+AE2=DE2.
由(1)知AE=DB,
∴AD2+DB2=DE2.
考点: 等腰直角三角形,三角形全等,勾股定理.

练习册系列答案
相关题目
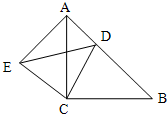 21、如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证:
21、如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证: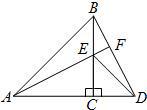 14、如图,△ACB和△ECD都是等腰直角三角形,A,C,D三点在同一直线上,连接BD,AE,并延长AE交BD于F.
14、如图,△ACB和△ECD都是等腰直角三角形,A,C,D三点在同一直线上,连接BD,AE,并延长AE交BD于F.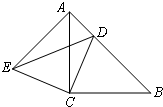 16、如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
16、如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.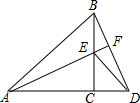 如图,△ACB和△ECD中,AC=BC,CE=CD,BC⊥AD,A、C、D三点在同一直线上,连接BD、AE,并延长交BD于F.
如图,△ACB和△ECD中,AC=BC,CE=CD,BC⊥AD,A、C、D三点在同一直线上,连接BD、AE,并延长交BD于F.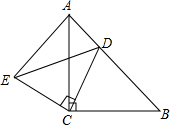 如图,△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°,D在AB上.
如图,△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°,D在AB上.