题目内容
如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,且AC=CD,AD= CD
CD
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
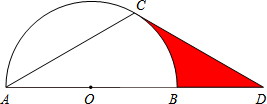
解:(1)连接OC,BC,
∵AC=CD,OA=OC,
∴∠A=∠D,∠A=∠OCA,
∴∠A=∠D=∠OCA,
∴△OAC∽△CAD,
∴AC:AD=OA:AC,
∵AD= CD,
CD,
∴OA:OC=1: ,
,
∵AB=2OA,
∴ =
= ,
,
∵AB是直径,
∴∠ACB=90°,且cos∠A= ,sin∠ABC=
,sin∠ABC= ,
,
∴∠A=∠ACO=∠D=30°,∠ABC=60°,
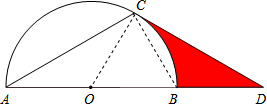 ∵OC=OB,
∵OC=OB,
∴△OBC是等边三角形,
∴∠BOC=60°,
∴∠OCB=180°-∠D-∠BOC=90°,
即OC⊥CD,
∵C在⊙O上,
∴CD是⊙O的切线;
(2)∵⊙O的半径为2,
∴OC=2,
在Rt△OCB中,∠D=30°,
∴CD= =2
=2 ,
,
∴S阴影=S△OCD-S扇形BOC= ×2×2
×2×2 -
- ×π×22=2
×π×22=2 -
- π.
π.
分析:(1)首先连接OC,BC,易证得△OAC∽△CAD,由AB是直径,易求得cos∠A= ,sin∠ABC=
,sin∠ABC= ,继而求得各角的度数,继而证得CD是⊙O的切线;
,继而求得各角的度数,继而证得CD是⊙O的切线;
(2)由⊙O的半径为2,利用三角函数的性质,可求得CD的长,然后由S阴影=S△OCD-S扇形BOC,求得答案.
点评:此题考查了切线的判定、相似三角形的判定与性质、等边三角形的判定与性质、扇形面积以及三角函数等知识.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.
∵AC=CD,OA=OC,
∴∠A=∠D,∠A=∠OCA,
∴∠A=∠D=∠OCA,
∴△OAC∽△CAD,
∴AC:AD=OA:AC,
∵AD=
 CD,
CD,∴OA:OC=1:
 ,
,∵AB=2OA,
∴
 =
= ,
,∵AB是直径,
∴∠ACB=90°,且cos∠A=
 ,sin∠ABC=
,sin∠ABC= ,
,∴∠A=∠ACO=∠D=30°,∠ABC=60°,
 ∵OC=OB,
∵OC=OB,∴△OBC是等边三角形,
∴∠BOC=60°,
∴∠OCB=180°-∠D-∠BOC=90°,
即OC⊥CD,
∵C在⊙O上,
∴CD是⊙O的切线;
(2)∵⊙O的半径为2,
∴OC=2,
在Rt△OCB中,∠D=30°,
∴CD=
 =2
=2 ,
,∴S阴影=S△OCD-S扇形BOC=
 ×2×2
×2×2 -
- ×π×22=2
×π×22=2 -
- π.
π.分析:(1)首先连接OC,BC,易证得△OAC∽△CAD,由AB是直径,易求得cos∠A=
 ,sin∠ABC=
,sin∠ABC= ,继而求得各角的度数,继而证得CD是⊙O的切线;
,继而求得各角的度数,继而证得CD是⊙O的切线;(2)由⊙O的半径为2,利用三角函数的性质,可求得CD的长,然后由S阴影=S△OCD-S扇形BOC,求得答案.
点评:此题考查了切线的判定、相似三角形的判定与性质、等边三角形的判定与性质、扇形面积以及三角函数等知识.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 28、如图所示,在直角坐标系中,矩形OBCD的边长OB=4,OD=2.
28、如图所示,在直角坐标系中,矩形OBCD的边长OB=4,OD=2.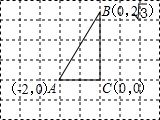 BC的2倍,“宝藏”就在矩形未知的顶点处,那么“宝藏”的位置可能是
BC的2倍,“宝藏”就在矩形未知的顶点处,那么“宝藏”的位置可能是 OB方向运动,运动速度是1个单位/秒,运动时间为t秒,直到点P与点B重合为止.
OB方向运动,运动速度是1个单位/秒,运动时间为t秒,直到点P与点B重合为止. (2013•龙湾区一模)如图,热气球从山顶A竖直上升至点B需25秒,点D在地面上,DC⊥AB,垂足为C,从地面上点D分别仰视A,B两点,测得∠ADC=20°,∠BDC=60°,若CD=130米.求该热气球从山顶A竖直上升至点B的平均速度.(结果精确到0.1米/秒)
(2013•龙湾区一模)如图,热气球从山顶A竖直上升至点B需25秒,点D在地面上,DC⊥AB,垂足为C,从地面上点D分别仰视A,B两点,测得∠ADC=20°,∠BDC=60°,若CD=130米.求该热气球从山顶A竖直上升至点B的平均速度.(结果精确到0.1米/秒)