题目内容
在⊙O的直径AB的延长线上取一点C,作⊙O的切线CD,D是切点,⊙O在B点的切线交CD于E,若CE=2•DE,则AC:CD=分析:根据切线长定理即可证得:DE=EB,在直角△BCE中,即可得到CE=2DE=2BE,而BC=
DE,根据切割线定理即可求得AC(用DE表示),即可求解.
| 3 |
解答: 解:设DE=x,则CE=2x,EB=x在Rt△EBC中,BC=
解:设DE=x,则CE=2x,EB=x在Rt△EBC中,BC=
x,
由切割线定理得9x2=
x•AC,
∴AC=3
x,
故AC:CD=3
x:3x=
:1.
 解:设DE=x,则CE=2x,EB=x在Rt△EBC中,BC=
解:设DE=x,则CE=2x,EB=x在Rt△EBC中,BC=| 3 |
由切割线定理得9x2=
| 3 |
∴AC=3
| 3 |
故AC:CD=3
| 3 |
| 3 |
点评:本题主要考查了切线长定理以及切割线定理,正确理解△BCE的边的关系是解决本题的关系.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
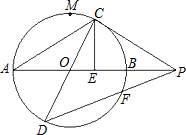 如图,已知AB=2,AB、CD是⊙O的两条直径,M为弧AB的中点,C在弧MB上运动,点P在AB的延长上,且PC=AC,作CE⊥AP于E,连接DP交⊙O于F.
如图,已知AB=2,AB、CD是⊙O的两条直径,M为弧AB的中点,C在弧MB上运动,点P在AB的延长上,且PC=AC,作CE⊥AP于E,连接DP交⊙O于F.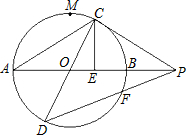 如图,已知AB=2,AB、CD是⊙O的两条直径,M为弧AB的中点,C在弧MB上运动,点P在AB的延长上,且PC=AC,作CE⊥AP于E,连接DP交⊙O于F.
如图,已知AB=2,AB、CD是⊙O的两条直径,M为弧AB的中点,C在弧MB上运动,点P在AB的延长上,且PC=AC,作CE⊥AP于E,连接DP交⊙O于F. 时,PC与⊙O相切;
时,PC与⊙O相切; 时,PC与⊙O相切;
时,PC与⊙O相切;