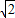题目内容
某校数学课外活动探究小组,在教师的引导下,对“函数y=x+
(x>0,k>0)的性质”作了如下探究:
因为y=x+
=(
)2-2
•
+(
)2+2
=(
-
)2+2
,
所以当x>0,k>0时,函数y=x+
有最小值2
,此时
=
,x=
.
借助上述性质:我们可以解决下面的问题:
某工厂要建造一个长方体无盖污水处理池,其容积为4800m3,深为3m,如果池底每平方米的造价为150元,池壁每平方米的造价为120元,问怎样设计水池能使总造价最低,最低总造价为______元.
| k |
| x |
因为y=x+
| k |
| x |
| x |
| x |
|
|
| k |
| x |
|
| k |
所以当x>0,k>0时,函数y=x+
| k |
| x |
| k |
| x |
|
| k |
借助上述性质:我们可以解决下面的问题:
某工厂要建造一个长方体无盖污水处理池,其容积为4800m3,深为3m,如果池底每平方米的造价为150元,池壁每平方米的造价为120元,问怎样设计水池能使总造价最低,最低总造价为______元.
由题意可得,池底面积为
=1600m3,
设池底一边长度为x.则另一边为
,
故可得出侧面积为:2×3x+2×3•
,
又∵池底每平方米的造价为150元,池壁每平方米的造价为120元,
∴总造价为:1600×150+(6x+
)×120
=240000+720x+
,
由题意条件:当x>0,k>0时,函数y=x+
有最小值2
,此时
=
,x=
.
故可得出总造价=240000+720x+
≥240000+2
=240000+57600=297600元.
故答案为:297600.
| 4800 |
| 3 |
设池底一边长度为x.则另一边为
| 1600 |
| x |
故可得出侧面积为:2×3x+2×3•
| 1600 |
| x |
又∵池底每平方米的造价为150元,池壁每平方米的造价为120元,
∴总造价为:1600×150+(6x+
| 9600 |
| x |
=240000+720x+
| 1152000 |
| x |
由题意条件:当x>0,k>0时,函数y=x+
| k |
| x |
| k |
| x |
|
| k |
故可得出总造价=240000+720x+
| 1152000 |
| x |
720x•
|
故答案为:297600.

练习册系列答案
相关题目
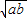 成立.某同学在做一个面积为3 600cm2,对角线相互垂直的四边形风筝时,运用上述规律,求得用来作对角线用的竹条至少需要准备xcm.则x的值是( )
成立.某同学在做一个面积为3 600cm2,对角线相互垂直的四边形风筝时,运用上述规律,求得用来作对角线用的竹条至少需要准备xcm.则x的值是( )
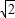
 成立.某同学在做一个面积为3 600cm2,对角线相互垂直的四边形风筝时,运用上述规律,求得用来作对角线用的竹条至少需要准备xcm.则x的值是( )
成立.某同学在做一个面积为3 600cm2,对角线相互垂直的四边形风筝时,运用上述规律,求得用来作对角线用的竹条至少需要准备xcm.则x的值是( )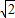

 成立.某同学在做一个面积为3 600cm2,对角线相互垂直的四边形风筝时,运用上述规律,求得用来作对角线用的竹条至少需要准备xcm.则x的值是( )
成立.某同学在做一个面积为3 600cm2,对角线相互垂直的四边形风筝时,运用上述规律,求得用来作对角线用的竹条至少需要准备xcm.则x的值是( )