题目内容
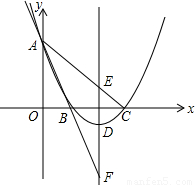
17、如图，已知：过?ABCD的对角线BD上一点O的直线分别交DA和BC的延长线于E、F．请问：OE与OF相等吗？若相等请证明，若不相等，需添加什么条件就能证得它们相等？请写出你的想法，再证明之．分析：当O是BD上任意一点时，OB和OD不一定相等，OE和OF也就没有确定的关系；当O是BD中点时，可以利用已知条件容易证明△ODE≌△OEF，根据全等三角形的性质就可以确定OE=OF．
解答：解：当O是BD上任意一点时，OE与OF不一定相等
当O是BD中点时，就可证得：OE=OF
证明：∵O是BD中点
∴OB=OD
又∵□ABCD中AD∥BC
∴∠ADB=∠DBC∠E=∠F，
∴△ODE≌△OEF
∴OE=OF
（本题答案不唯一）
当O是BD中点时，就可证得：OE=OF
证明：∵O是BD中点
∴OB=OD
又∵□ABCD中AD∥BC
∴∠ADB=∠DBC∠E=∠F，
∴△ODE≌△OEF
∴OE=OF
（本题答案不唯一）
点评：此题是开放性试题，题目主要考查了全等三角形的性质与判定、平行四边形的性质，首先利用平行四边形的性质构造全等条件，然后利用全等三角形的性质解决问题．
练习册系列答案
阅读快车系列答案
相关题目
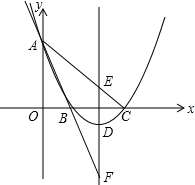如图，已知抛物线过点A（0，6），B（2，0），C（6，0），直线AB交抛物线的对称轴于点F，直线AC交抛物线对称轴于点E．
如图，已知，直线AB、CD相交于点O，OE平分∠BOD，∠AOC=60°，过点O作OF⊥CD．求∠EOF的度数．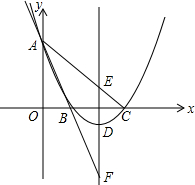
如图，已知抛物线过点A（0，6），B（2，0），C（6，0），直线AB交抛物线的对称轴于点F，直线AC交抛物线对称轴于点E．