题目内容
 如图,D是线段AB上的一点,BD=2AD=4,以BD为直径作半圆O,过点A作半圆O的切线,切点为E,过点B作BC⊥AE于C交半圆于F,连接EF.有下列四个结论:
如图,D是线段AB上的一点,BD=2AD=4,以BD为直径作半圆O,过点A作半圆O的切线,切点为E,过点B作BC⊥AE于C交半圆于F,连接EF.有下列四个结论:①∠A=30°;②BF=3CF;③
 |
| DE |
 |
| EF |
其中正确的结论是
①③④
①③④
.分析:①由切线的性质和解直角三角形得到∠A=30°;
②如图,连接DF.根据圆周角定理和平行线的判定推知AC∥DF,则平行线分线段成比例,即
=
,由此可以求得BF=2CF;
③由平行线的性质得到DF⊥OE,则根据垂径定理和圆周角、弧、弦的关系进行解答;
④由圆周角、弧、弦的关系和旋切角定理求得内错角∠CEF=∠EFD,则EF∥AB.
②如图,连接DF.根据圆周角定理和平行线的判定推知AC∥DF,则平行线分线段成比例,即
| BF |
| BC |
| BD |
| BA |
③由平行线的性质得到DF⊥OE,则根据垂径定理和圆周角、弧、弦的关系进行解答;
④由圆周角、弧、弦的关系和旋切角定理求得内错角∠CEF=∠EFD,则EF∥AB.
解答: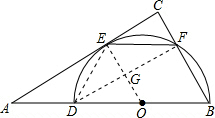 解:①如图,连接OE.
解:①如图,连接OE.
∵AE是切线,
∴AE⊥OE,即∠AEO=90°.
∵BD=2AD=4,
∴OE=OD=2,
∴AO=AD+OD=2OE,
∴∠A=30°;
故①正确;
②如图,连接DF.
∵BD是直径,∴DF⊥EF.
又∵AC⊥BC,
∴AC∥DF,
∴
=
,由比例的性质得到
=
=2,即BF=2CF.故②错误;
③如图,假设DF交OE于点G.
∵AC∥DF,AE⊥OE,
∴DF⊥OE,
∴DG=FG,
∴
=
.
故③正确;
④如图,连接DE.
∵
=
.
∴∠EDF=∠EFD.
又∵AC是切线,
∴∠CEF=∠EDF,
∴∠CEF=∠EFD,
∴EF∥AB.
故④正确.
综上所述,正确的结论是①③④.
故答案是:①③④.
 解:①如图,连接OE.
解:①如图,连接OE.∵AE是切线,
∴AE⊥OE,即∠AEO=90°.
∵BD=2AD=4,
∴OE=OD=2,
∴AO=AD+OD=2OE,
∴∠A=30°;
故①正确;
②如图,连接DF.
∵BD是直径,∴DF⊥EF.
又∵AC⊥BC,
∴AC∥DF,
∴
| BF |
| BC |
| BD |
| BA |
| BF |
| CF |
| BD |
| DA |
③如图,假设DF交OE于点G.
∵AC∥DF,AE⊥OE,
∴DF⊥OE,
∴DG=FG,
∴
 |
| DE |
 |
| EF |
故③正确;
④如图,连接DE.
∵
 |
| DE |
 |
| EF |
∴∠EDF=∠EFD.
又∵AC是切线,
∴∠CEF=∠EDF,
∴∠CEF=∠EFD,
∴EF∥AB.
故④正确.
综上所述,正确的结论是①③④.
故答案是:①③④.
点评:本题综合考查了切线的性质,圆周角定理以及垂径定理等知识点.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 23、如图,C是线段AB上一点,分别以AC、BC为边在线段AB同侧作正方形ACDE和BCFG,连接AF、BD.
23、如图,C是线段AB上一点,分别以AC、BC为边在线段AB同侧作正方形ACDE和BCFG,连接AF、BD. 、BE.
、BE. 如图,C是线段AB上的一点,△ACD和△BCE都是等边三角形.
如图,C是线段AB上的一点,△ACD和△BCE都是等边三角形.