题目内容
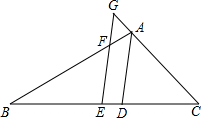
 如图,在⊙O中,AB=AC,则△ABD∽________;若AC=12,AE=8,则AD=________.
如图,在⊙O中,AB=AC,则△ABD∽________;若AC=12,AE=8,则AD=________.
△AEB 18
分析:由同弧所对的圆周角相等可知,∠D=∠C,由AB=AC,∠ABC=∠C可推出△ABD∽△AEB,利用相似三角形对应边成比例即可得出答案.
解答:∵AB=AC,
∴∠ABC=∠C,
∵∠D=∠C(同弧所对的圆周角相等),
∴∠ABC=∠D,
∵∠BAD=∠EAB,
∴△ABD∽△AEB,
∴ =
= ,
,
即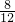 =
= ,
,
解得AD=18.
故答案为:18.
点评:此题主要考查学生对相似三角形的判定与性质和相交弦定理的理解和应用,解题时注意找准相似三角形.如果利用△ABD∽△ABC,再求AD的长就比较麻烦了.
分析:由同弧所对的圆周角相等可知,∠D=∠C,由AB=AC,∠ABC=∠C可推出△ABD∽△AEB,利用相似三角形对应边成比例即可得出答案.
解答:∵AB=AC,
∴∠ABC=∠C,
∵∠D=∠C(同弧所对的圆周角相等),
∴∠ABC=∠D,
∵∠BAD=∠EAB,
∴△ABD∽△AEB,
∴
 =
= ,
,即
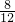 =
= ,
,解得AD=18.
故答案为:18.
点评:此题主要考查学生对相似三角形的判定与性质和相交弦定理的理解和应用,解题时注意找准相似三角形.如果利用△ABD∽△ABC,再求AD的长就比较麻烦了.

练习册系列答案
相关题目
 如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.
如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G. 如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠EDC=33°,则∠DAE的度数为
如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠EDC=33°,则∠DAE的度数为 如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.
如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.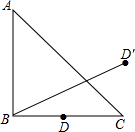 如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′=
如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′=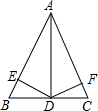 如图,在△ABC中,AB=AC,D点是BC的中点,DE⊥AB于E点,DF⊥AC于F点,则图中全等三角形共有
如图,在△ABC中,AB=AC,D点是BC的中点,DE⊥AB于E点,DF⊥AC于F点,则图中全等三角形共有