题目内容
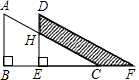 如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,EH=7,平移距离是5,则图中阴影部分的面积为________.
如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,EH=7,平移距离是5,则图中阴影部分的面积为________.
42.5
分析:易证△ABC∽△HEC,根据相似三角形的对应边的比相等,即可求得EC的长,则可以求得△DEF与△HEC的面积,两者的面积的差就是所求的阴影部分的面积.
解答:∵AB∥HE,
∴△ABC∽△HEC,
∴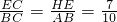 ,
,
∴设EC=x,则BC=5+x,则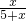 =
= ,
,
解得:x= .
.
∴BC=5+ =
= .
.
∴S△ABC=S△DEF= AB•BC=
AB•BC= ×10×
×10× =
= ,
,
S△HEC= HE•EC=
HE•EC= ×7×
×7× =
= .
.
∴阴影部分的面积为S△DEF-S△HEC= -
- =42.5.
=42.5.
故答案是:42.5.
点评:本题考查了相似三角形的判定与性质,利用相似三角形的对应边的比相等,正确求得EC的长度是关键.
分析:易证△ABC∽△HEC,根据相似三角形的对应边的比相等,即可求得EC的长,则可以求得△DEF与△HEC的面积,两者的面积的差就是所求的阴影部分的面积.
解答:∵AB∥HE,
∴△ABC∽△HEC,
∴
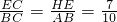 ,
,∴设EC=x,则BC=5+x,则
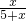 =
= ,
,解得:x=
 .
.∴BC=5+
 =
= .
.∴S△ABC=S△DEF=
 AB•BC=
AB•BC= ×10×
×10× =
= ,
,S△HEC=
 HE•EC=
HE•EC= ×7×
×7× =
= .
.∴阴影部分的面积为S△DEF-S△HEC=
 -
- =42.5.
=42.5.故答案是:42.5.
点评:本题考查了相似三角形的判定与性质,利用相似三角形的对应边的比相等,正确求得EC的长度是关键.

练习册系列答案
相关题目
 如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=3,平移距离是5,则图中阴影部分的面积为
如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=3,平移距离是5,则图中阴影部分的面积为

