题目内容
 如图,在菱形ABCD中,∠B=60°,点E、F分别是BC、DC上的动点,且BE=DF.某小组的同学观察图形得出五个结论:①AE=AF;②∠CEF=∠CFE;③△AEF≌△CEF;④当点E、F分别是边BC、DC中点时,△AEF是等边三角形;⑤当点E在边BC上且点F在边DC上,且满足BE=DF时,△AEF的面积为定值.其中,真命题是________(写出所有真命题的序号).
如图,在菱形ABCD中,∠B=60°,点E、F分别是BC、DC上的动点,且BE=DF.某小组的同学观察图形得出五个结论:①AE=AF;②∠CEF=∠CFE;③△AEF≌△CEF;④当点E、F分别是边BC、DC中点时,△AEF是等边三角形;⑤当点E在边BC上且点F在边DC上,且满足BE=DF时,△AEF的面积为定值.其中,真命题是________(写出所有真命题的序号).
①②
分析:根据菱形的性质可证明△ABE≌△ADF,则AE=AF;CE=CF,∠CEF=∠CFE,当点E,F分别为边BC,DC的中点时,BE= AB,DF=
AB,DF= AD,无法求出∠EAF的度数,再由△AEF的面积=菱形ABCD的面积-△ABE的面积-△ADF的面积-△CEF的面积,即可得出△AEF的面积是BE的二次函数,即可求出,△AEF的面积最大.
AD,无法求出∠EAF的度数,再由△AEF的面积=菱形ABCD的面积-△ABE的面积-△ADF的面积-△CEF的面积,即可得出△AEF的面积是BE的二次函数,即可求出,△AEF的面积最大.
解答: 解:∵点E、F分别从点B、D出发以同样的速度沿边BC、DC向点C运动,
解:∵点E、F分别从点B、D出发以同样的速度沿边BC、DC向点C运动,
∴BE=DF,
∵AB=AD,∠B=∠D,
∴△ABE≌△ADF,
∴AE=AF,①正确;
∴CE=CF,
∴∠CEF=∠CFE,②正确;③错误;
当点E,F分别为边BC,DC的中点时,BE= AB,DF=
AB,DF= AD,
AD,
无法得出∠EAF的度数,④错误;
∵△AEF的面积=菱形ABCD的面积-△ABE的面积-△ADF的面积-△CEF的面积,
= AB2-
AB2- BE•AB×
BE•AB× ×2-
×2- ×
× ×(AB-BE)2,
×(AB-BE)2,
=- BE2+
BE2+ AB2,
AB2,
∴△AEF的面积是BE的二次函数,
∴当BE=0时,△AEF的面积最大,⑤错误.
故正确的序号有①②.
点评:本题考查了菱形的性质、全等三角形的判定和等边三角形的判定,是中考压轴题,难度较大.
分析:根据菱形的性质可证明△ABE≌△ADF,则AE=AF;CE=CF,∠CEF=∠CFE,当点E,F分别为边BC,DC的中点时,BE=
 AB,DF=
AB,DF= AD,无法求出∠EAF的度数,再由△AEF的面积=菱形ABCD的面积-△ABE的面积-△ADF的面积-△CEF的面积,即可得出△AEF的面积是BE的二次函数,即可求出,△AEF的面积最大.
AD,无法求出∠EAF的度数,再由△AEF的面积=菱形ABCD的面积-△ABE的面积-△ADF的面积-△CEF的面积,即可得出△AEF的面积是BE的二次函数,即可求出,△AEF的面积最大.解答:
 解:∵点E、F分别从点B、D出发以同样的速度沿边BC、DC向点C运动,
解:∵点E、F分别从点B、D出发以同样的速度沿边BC、DC向点C运动,∴BE=DF,
∵AB=AD,∠B=∠D,
∴△ABE≌△ADF,
∴AE=AF,①正确;
∴CE=CF,
∴∠CEF=∠CFE,②正确;③错误;
当点E,F分别为边BC,DC的中点时,BE=
 AB,DF=
AB,DF= AD,
AD,无法得出∠EAF的度数,④错误;
∵△AEF的面积=菱形ABCD的面积-△ABE的面积-△ADF的面积-△CEF的面积,
=
 AB2-
AB2- BE•AB×
BE•AB× ×2-
×2- ×
× ×(AB-BE)2,
×(AB-BE)2,=-
 BE2+
BE2+ AB2,
AB2,∴△AEF的面积是BE的二次函数,
∴当BE=0时,△AEF的面积最大,⑤错误.
故正确的序号有①②.
点评:本题考查了菱形的性质、全等三角形的判定和等边三角形的判定,是中考压轴题,难度较大.

练习册系列答案
相关题目
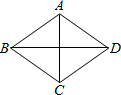 如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )
如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )| A、5 | B、10 | C、6 | D、8 |
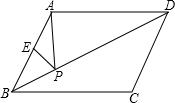
 ME交射线CD于点N,连接MD、AN.
ME交射线CD于点N,连接MD、AN. (2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA=
(2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA= 如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.
如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.