题目内容
直角三角形的两直角边是3,4,则以斜边长为直径的圆的面积是________.

分析:设三角形的斜边长为c,由勾股定理可得c2=32+42,由此可求出斜边的长,以斜边长为直径,则半径为r=
 ,根据圆的面积=πr2,将r代入面积公式可求出该圆的面积.
,根据圆的面积=πr2,将r代入面积公式可求出该圆的面积.解答:设斜边长为c,由勾股定理得:
c2=32+42,c=5.
所以,以斜边长为直径的圆的面积是:π×(
 )2=
)2= .
.点评:本题主要考查勾股定理和圆的面积公式,由勾股定理求出该圆的直径,代入圆的面积公式求出该圆的面积.

练习册系列答案
相关题目
 ,
, 表示直角三角形的两直角边(
表示直角三角形的两直角边( ),下列四个说法:
),下列四个说法:
 ,②
,② ,③
,③ ,④
,④ .
.
 ,
,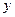 表示直角三角形的两直角边(
表示直角三角形的两直角边( ),下列四个说法:
),下列四个说法: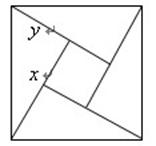
 ,②
,② ,③
,③ ,④
,④ .
.