题目内容
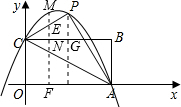
如图,矩形OABC的长OA=
,宽OC=1,将△AOC沿AC翻折得△APC.
(1)填空:∠PCB=______度,P点坐标为______;
(2)若P、A两点在抛物线y=-
x2+bx+c上,求b,c的值;
(3)若直线y=kx+m平行于CP,且于(2)中的抛物线有且只有一个交点,求k,m的值;
(4)在(2)中抛物线CP段(不包括C,P点)上,是否存在一点M,使得四边形MCAP的面积最大?若存在求此时M的坐标;若不存在,请说明理由.

| 3 |
(1)填空:∠PCB=______度,P点坐标为______;
(2)若P、A两点在抛物线y=-
| 4 |
| 3 |
(3)若直线y=kx+m平行于CP,且于(2)中的抛物线有且只有一个交点,求k,m的值;
(4)在(2)中抛物线CP段(不包括C,P点)上,是否存在一点M,使得四边形MCAP的面积最大?若存在求此时M的坐标;若不存在,请说明理由.

(1)过点P作PG⊥x轴交CB于G.
tan∠CAO=
=
,
∴∠CAO=30°,
∴PCA=60°,
又∵∠ACB=30°,
∴∠PCB=30°,
在RT△PCM中,PG=
PC=
OC=
,GC=
,
∴点P的坐标为(
,
).
综上可得:∠PCB=30°,P点坐标为(
,
).
(2)把P(
,
)与A(
,0)分别代入y=-
x2+bx+c,
解得:b=
,c=1,
∴y=-
x2+
x+1,
(3)由P(
,
),C(0,1)可得直线CP:y=
x+1,
∵直线y=kx+m平行于CP,
∴k=
,
∵y=
x+m与y=-
x2+
x+1只有一个交点,
∴-
x2+
x+1=
x+m有两个相同的实数根(
)2-4×
×(m-1)=0,
解得:m=
;…(3分)
(4)假设存在这样的点M,使得四边形MCAP的面积最大.
∵△ACP面积为定值,
∴要使四边形MCAP的面积最大,只需使△PCM的面积最大.
过点M作MF⊥x轴分别交CP、CB和x轴于E、N和F,过点P作PG⊥x轴交CB于G.
S△CMP=s△CME+S△PME=
ME•CG=
ME
设M(x0,y0),
∵∠ECN=30°,CN=x0,
∴EN=
x0
∴ME=MF-EF=-
x02+
x0
∴S△CMP=-
x02+
x
∵a=-
<0,
∴S有最大值.
当x0=
时,S的最大值是
,
∵S△MCAP=S△CPM+S△ACP
∴四边形MCAP的面积的最大值为
此时M点的坐标为(
,
)
所以存在这样的点M(
,
),使得四边形MCAP的面积最大,其最大值为
.
tan∠CAO=
| OC |
| OA |
| ||
| 3 |
∴∠CAO=30°,
∴PCA=60°,
又∵∠ACB=30°,
∴∠PCB=30°,
在RT△PCM中,PG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴点P的坐标为(
| ||
| 2 |
| 3 |
| 2 |
综上可得:∠PCB=30°,P点坐标为(
| ||
| 2 |
| 3 |
| 2 |
(2)把P(
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
解得:b=
| 3 |
∴y=-
| 4 |
| 3 |
| 3 |
(3)由P(
| ||
| 2 |
| 3 |
| 2 |
| ||
| 3 |
∵直线y=kx+m平行于CP,
∴k=
| ||
| 3 |
∵y=
| ||
| 3 |
| 4 |
| 3 |
| 3 |
∴-
| 4 |
| 3 |
| 3 |
| ||
| 3 |
2
| ||
| 3 |
| 4 |
| 3 |
解得:m=
| 5 |
| 4 |
(4)假设存在这样的点M,使得四边形MCAP的面积最大.
∵△ACP面积为定值,
∴要使四边形MCAP的面积最大,只需使△PCM的面积最大.
过点M作MF⊥x轴分别交CP、CB和x轴于E、N和F,过点P作PG⊥x轴交CB于G.

S△CMP=s△CME+S△PME=
| 1 |
| 2 |
| ||
| 4 |
设M(x0,y0),
∵∠ECN=30°,CN=x0,
∴EN=
| ||
| 3 |
∴ME=MF-EF=-
| 4 |
| 3 |
2
| ||
| 3 |
∴S△CMP=-
| ||
| 3 |
| 1 |
| 2 |
∵a=-
| ||
| 3 |
∴S有最大值.
当x0=
| ||
| 4 |
| ||
| 16 |
∵S△MCAP=S△CPM+S△ACP
∴四边形MCAP的面积的最大值为
9
| ||
| 16 |
此时M点的坐标为(
| ||
| 4 |
| 3 |
| 2 |
所以存在这样的点M(
| ||
| 4 |
| 3 |
| 2 |
9
| ||
| 16 |

练习册系列答案
相关题目





 、
、 等,这些牌照中的5个数字都是关于中间的一个数字“对称”的,给人以对称美的享受,我们不妨把这样的牌照叫作“数字对称”牌照,如果让你负责制作以8或9开头且有5个数字的“数字对称”牌照,那么最多可制作( )
等,这些牌照中的5个数字都是关于中间的一个数字“对称”的,给人以对称美的享受,我们不妨把这样的牌照叫作“数字对称”牌照,如果让你负责制作以8或9开头且有5个数字的“数字对称”牌照,那么最多可制作( )
