题目内容
如图,直线y= x-3分别与y轴、x轴交于点A,B,抛物线y=-
x-3分别与y轴、x轴交于点A,B,抛物线y=- x2+2x+2与y轴交于点C,此抛物线的对称轴分别与BC,x轴交于点P,Q.
x2+2x+2与y轴交于点C,此抛物线的对称轴分别与BC,x轴交于点P,Q.(1)求证:AB=AC;
(2)求证:AP垂直平分线段BC.

【答案】分析:(1)根据已知条件可以求出点A、B、C的坐标,从而求出OC、OA、OB的长,再求出AC的长,由勾股定理求出AB的长,从而可以得出结论.
(2)根据抛物线的解析式求出对称轴,从而求出Q点的坐标,求出OQ、BQ的值,利用直线平行证明三角形相似从而求出P是BC的中点,根据等腰三角形的性质可以得出结论.
解答:证明:(1)∵y= x-3,
x-3,
∴x=0时,y=-3,
∴A(0,-3),
当y=0时,x=4,
∴B(4,0),
∵y=- x2+2x+2,
x2+2x+2,
∴x=0时,y=2,
∴C(0,2).
∴OA=3,OB=4,OC=2.
∴AC=OA+OC=5.
AB= =
=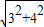 =5.
=5.
∴AB=AC.
(2)∵抛物线y=- x2+2x+2,
x2+2x+2,
∴y=- (x2-4x+4-4)+2
(x2-4x+4-4)+2
=- (x-2)2+4
(x-2)2+4
∴对称轴是直线x=2,
∴点Q的坐标为(2,0).
∴OQ=BQ=2.
∵PQ∥y轴,
∴△BPQ∽△BCO.
∴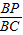 =
=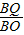 =
= =
= .
.
∴BP=PC,
∵AB=AC,∴AP⊥BC.
∴AP垂直平分线段BC.
点评:本题是一道二次函数、一次函数的综合试题,考查了等腰三角形的判定,相似三角形的判定与性质,函数图象上点的坐标特征及勾股定理的运用.
(2)根据抛物线的解析式求出对称轴,从而求出Q点的坐标,求出OQ、BQ的值,利用直线平行证明三角形相似从而求出P是BC的中点,根据等腰三角形的性质可以得出结论.
解答:证明:(1)∵y=
 x-3,
x-3,∴x=0时,y=-3,
∴A(0,-3),
当y=0时,x=4,
∴B(4,0),
∵y=-
 x2+2x+2,
x2+2x+2,∴x=0时,y=2,
∴C(0,2).
∴OA=3,OB=4,OC=2.
∴AC=OA+OC=5.
AB=
 =
=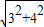 =5.
=5.∴AB=AC.
(2)∵抛物线y=-
 x2+2x+2,
x2+2x+2,∴y=-
 (x2-4x+4-4)+2
(x2-4x+4-4)+2=-
 (x-2)2+4
(x-2)2+4∴对称轴是直线x=2,
∴点Q的坐标为(2,0).
∴OQ=BQ=2.
∵PQ∥y轴,
∴△BPQ∽△BCO.
∴
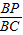 =
=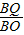 =
= =
= .
.∴BP=PC,
∵AB=AC,∴AP⊥BC.
∴AP垂直平分线段BC.
点评:本题是一道二次函数、一次函数的综合试题,考查了等腰三角形的判定,相似三角形的判定与性质,函数图象上点的坐标特征及勾股定理的运用.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目

 13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( )
13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( ) 4、如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为( )
4、如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为( ) 如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数
如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数 17、如图,直线a∥c,b∥c,直线d与直线a、b、c相交,已知∠1=60°,求∠2、∠3的度数(可在图中用数字表示角).
17、如图,直线a∥c,b∥c,直线d与直线a、b、c相交,已知∠1=60°,求∠2、∠3的度数(可在图中用数字表示角).