题目内容
矩形的两条对角线所夹的一个锐角为60°，那么矩形较短边与较长边的比是
- A.1：2
- B.
：1 - C.：3
- D.1：3
C
分析：本题首先求出矩形的两条对角线所夹的各个夹角的度数，再求较短边与较长边的比．
解答：
解：如图，已知矩形的两条对角线所夹的一个锐角为60°，
根据矩形的性质可得∠OAB=∠OBA=60°，
所以∠BDA=30°，
根据直角三角形的性质可得AB：AD=1：=
．
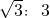故选C．
点评：此类题考查的是矩形的性质以及直角三角形的性质，难度一般．
分析：本题首先求出矩形的两条对角线所夹的各个夹角的度数，再求较短边与较长边的比．
解答：
解：如图，已知矩形的两条对角线所夹的一个锐角为60°，根据矩形的性质可得∠OAB=∠OBA=60°，
所以∠BDA=30°，
根据直角三角形的性质可得AB：AD=1：
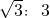=．故选C．
点评：此类题考查的是矩形的性质以及直角三角形的性质，难度一般．
练习册系列答案
名校课堂系列答案
相关题目
矩形的两条对角线所夹的一个锐角为60°，那么矩形较短边与较长边的比是（ ）
| A、1：2 | ||
B、
| ||
C、
| ||
| D、1：3 |
，较短的边长为12，则对角线长为 。