题目内容
19.直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).(1)求直线AB的解析式;
(2)在直线AB上是否存在点P,使△POA是等腰三角形?如存在,请画出所有满足条件的点P,并保留作图痕迹,如不存在,请说明理由.
分析 (1)AB的解析式为y=kx+b(k≠0),将点A(1,0)、点B(0,-2)分别代入解析式即可组成方程组,从而得到AB的解析式;
(2)设直线根据OA是底和OA是腰的时候,进行画图.根据等腰三角形的性质进行求解.
解答 解:(1)设直线AB的解析式为y=kx+b(k≠0).
∵直线AB过点A(1,0)、点B(0,-2),
∴$\left\{\begin{array}{l}{k+b=0}\\{b=-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=2}\\{b=-2}\end{array}\right.$,
∴直线AB的解析式为y=2x-2.
(2)①当OA是底时,则作OA的垂直平分线和AB的交点即是点P1的一个位置.
②当OA是腰时,以A为圆心,以OA为半径画弧,交直线AB于点P2、P4.以O为圆心,以OA为半径画弧,交直线AB于点P3.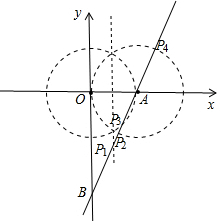
点评 本题考查了待定系数法求函数解析式以及等腰三角形的判定和性质,解答此题不仅要熟悉待定系数法,还要熟悉等腰三角形的判定和性质.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
9.观察下列标志,从图案看既是轴对称图形又是中心对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,BD是等腰Rt△ABC斜边AC上的高,AE平分∠BAC,交BC于点E,交BD于点F.求证:CE=2DF.
如图,BD是等腰Rt△ABC斜边AC上的高,AE平分∠BAC,交BC于点E,交BD于点F.求证:CE=2DF.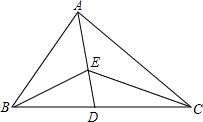 如图,AD为△ABC的角平分线,点E在AD上.
如图,AD为△ABC的角平分线,点E在AD上.