��Ŀ����
����Ŀ����ͼ����������![]() ��
��![]() ���㣬�ֱ��Ӧ����Ϊ
���㣬�ֱ��Ӧ����Ϊ![]() ��
��![]() ����֪
����֪![]() ��
��![]() ��Ϊ�෴������
��Ϊ�෴������![]() Ϊ������һ���㣬��ӦΪ
Ϊ������һ���㣬��ӦΪ![]() ��
��
(1)����![]() ����
����![]() �͵�
�͵�![]() �ľ�����ȣ����
�ľ�����ȣ����![]() ��Ӧ������
��Ӧ������
(2)�������Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() ����
����![]() �͵�
�͵�![]() �ľ���֮��Ϊ5?�����ڣ������
�ľ���֮��Ϊ5?�����ڣ������![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
(3)����![]() ��ÿ����1����λ���ȵ��ٶȴ�
��ÿ����1����λ���ȵ��ٶȴ�![]() �������˶�����
�������˶�����![]() ��ÿ����5����λ���������˶�����
��ÿ����5����λ���������˶�����![]() ��ÿ����20����λ���ȵ��ٶ������˶����ʼ�����ʱ��
��ÿ����20����λ���ȵ��ٶ������˶����ʼ�����ʱ��![]() ����
����![]() ����
����![]() �ľ�����ȣ�
�ľ�����ȣ�

���𰸡���1��1����2�����ڣ�-1.5��3.5����3����![]() ���ӻ�
���ӻ�![]() ����ʱ������ȣ�
����ʱ������ȣ�
��������
��1������P��A�뵽B������ȣ����x��ֵ�����ɵó�P��Ӧ������
��2�����������г�����x�ķ��̣�������̵Ľ⼴�ɵõ������
��3����y����ʱ��P����A����B�ľ�����ȣ����������г�����y�ķ��̣�������̵Ľ⼴�ɵõ������
��1���ߣ�a+1��2��|b-3|��Ϊ�෴����
��![]()
��a=-1��b=3��
��P���Ӧ����Ϊx��
��������ã�x+1=3-x��
��ã�x=1��
��P��Ӧ����Ϊ��1��
��2�����ڣ������ǣ�
��������ã�![]() ��
��
��![]() ʱ������ã�
ʱ������ã�![]() ����
����![]() ��
��
��![]() ʱ������ã�
ʱ������ã�![]() ����
����![]() ��
��
��3�����![]() ����ʱ����P����A����B�ľ�����ȣ�
����ʱ����P����A����B�ľ�����ȣ�
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
��![]() ʱ��
ʱ��
��ã�![]() ��
��
��![]() ʱ��
ʱ��
��ã�![]() ��
��
����![]() ���ӻ�
���ӻ�![]() ����ʱ������ȣ�
����ʱ������ȣ�

 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�����Ŀ��ij��·�ų�1000�ף�����һ�л���������ͨ������ûӿ�ʼ���ŵ���ȫͨ���Ź�����1���ӣ����ӳ�ͷ������ͷ����β�뿪��β������������ȫ�����ϵ�ʱ��Ϊ40�룮
��1����������лij���Ϊx�ף���д�±�������Ҫ����
����ʻ���� | ʱ�䣨�룩 | ·�̣��ף� | �ٶȣ���/�룩 |
��ȫͨ���� | 60 | ||
��������� | 40 |
��2�������лij��ȣ�
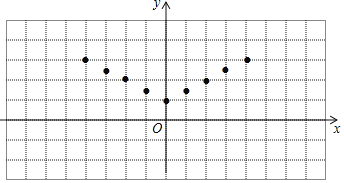
����Ŀ��ijУ��ѧ��ȤС�����ѧϰ�����ľ��飬�Ժ���y��![]() |x|+1��ͼ������ʽ�����̽����̽���������£���1���Ա���x��ȡֵ��Χ��ȫ��ʵ����x��y�ļ����Ӧֵ�����
|x|+1��ͼ������ʽ�����̽����̽���������£���1���Ա���x��ȡֵ��Χ��ȫ��ʵ����x��y�ļ����Ӧֵ�����
X | �� | ��4 | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | 4 | �� |
Y | �� | 3 | 2.5 | m | 1.5 | 1 | 1.5 | 2 | 2.5 | 3 | �� |
��1������m���� ����
��2����ͼ����ƽ��ֱ������ϵxOy�У�������ϱ��и��Զ�ӦֵΪ����ĵ㣬��������ĵ㣬�����ú�����ͼ��
��3����2��y��3ʱ��x��ȡֵ��ΧΪ�� ����