题目内容
在函数
中，y随x的增大而增大，则k的值可能是
- A.1
- B.
- C.2
- D.
D
分析：一次函数y=kx+b（k≠0），若y随x的增大而增大，则k＞0．
解答：y=（k-1-）x，当k=1，2，时，k-1-＜0，所以A，B，C错误，
当k=时，k-1-＞0，所以D对．
故选D．
点评：对于一次函数y=kx+b（k≠0）．当k＞0时，y随x的增大而增大，当k＜0时，y随x的增大而减小．b＞0，图象与y轴的正半轴相交，b=0，图象过原点，b＜0，图象与y轴的负半轴相交．
分析：一次函数y=kx+b（k≠0），若y随x的增大而增大，则k＞0．
解答：y=（k-1-
）x，当k=1，2，时，k-1-＜0，所以A，B，C错误，当k=
时，k-1-＞0，所以D对．故选D．
点评：对于一次函数y=kx+b（k≠0）．当k＞0时，y随x的增大而增大，当k＜0时，y随x的增大而减小．b＞0，图象与y轴的正半轴相交，b=0，图象过原点，b＜0，图象与y轴的负半轴相交．
练习册系列答案
阅读快车系列答案
相关题目
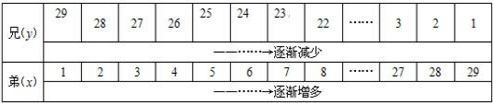
（1）兄弟二人分吃一碗饺子，每人吃饺子的个数如下表：
| 兄（y） | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | …… | 3 | 2 | 1 |
| ——……→逐渐减少 | ||||||||||||
| 弟（x） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | …… | 27 | 28 | 29 |
| ——……→逐渐增多 | ||||||||||||
①写出兄吃饺子数
与弟吃饺子数x之间的函数关系式（不要求写
的取值范围）.
②虽然当弟吃的饺子个数增多时，兄吃的饺子数()在减少，但与x是成反例吗？
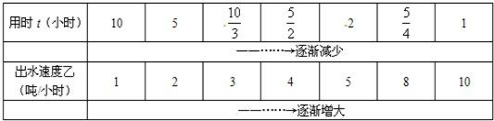
（2）水池中有水若干吨，若单开一个出水口，水流速v与全池水放光所用时t如下表：
| 用时t（小时） | 10 | 5 |
|
| 2 |
| 1 |
| ——……→逐渐减少 | |||||||
| 出水速度乙（吨/小时） | 1 | 2 | 3 | 4 | 5 | 8 | 10 |
| ——……→逐渐增大 | |||||||
①写出放光池中水用时t(小时)与放水速度v(吨/小时)之间的函数关系.
②这是一个反比例函数吗？
③与（1）的结论相比，可见并非反比例函数有可能“函数值随自变量增大而减小”，反之，所有的反比例函数都是“函数值随自变量的增大而减小吗？这个问题，你可以提前探索、尝试，也可以预习下一课时”反比例函数的图象和性质，也可以等到下一节课我们共同解决.