题目内容
某校要求学生每天坚持跑步锻炼，下课后学生在规定时间跑步来到操场，锻炼一段时间后，学生慢步回到教室，下面能反映某个学生离教室的距离y与时间x的函数关系的大致图象（ ）
A、 |
B、 |
C、 |
D、 |
考点：函数的图象
专题：
分析：根据在每段中，离家的距离随时间的变化情况即可进行判断．
解答：解：图象应分三个阶段，
第一阶段：跑步来到操场，在这个阶段，离教室的距离随时间的增大而增大；
第二阶段：锻炼一段时间，这一阶段离教室的距离不随时间的变化而改变．故D错误；
第三阶段：慢步回到教室，这一阶段，离教室的距离随时间的增大而减小，故A错误，并且这段的速度小于第一阶段的速度，则C错误．
故选B．
第一阶段：跑步来到操场，在这个阶段，离教室的距离随时间的增大而增大；
第二阶段：锻炼一段时间，这一阶段离教室的距离不随时间的变化而改变．故D错误；
第三阶段：慢步回到教室，这一阶段，离教室的距离随时间的增大而减小，故A错误，并且这段的速度小于第一阶段的速度，则C错误．
故选B．
点评：考查了函数的图象，理解每阶段中，离家的距离与时间的关系，根据图象的斜率判断运动的速度是解决本题的关键．
练习册系列答案
相关题目
化简-a
的结果是（ ）
-
|
A、
| ||
B、
| ||
C、-
| ||
D、-
|
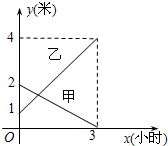自来水公司有甲、乙两个长方体的蓄水池，现将甲池中的水以每小时8m3的速度注入乙池，则两水池中水的高度y（m）与注水的时间x（h）之间的函数图象如图所示．若要乙池的蓄水量是甲池的2倍，则注水的时间应为（ ）| A、2h | ||
B、
| ||
C、
| ||
D、
|
若式子
在实数范围内有意义，则x满足（ ）
| 1 | ||
|
A、x＞
| ||
B、x＜
| ||
C、x≤
| ||
D、x≥
|
在数4，-1，3，-6中，其中最小的是（ ）
| A、-6 | B、-4 | C、-1 | D、6 |
在
，-2.5，4，
四个数中，无理数是（ ）
| 5 |
| 1 |
| 3 |
A、
| ||
| B、-2.5 | ||
| C、4 | ||
D、
|
某几何体的三视图如图所示，则这个几何体是（ ）A、 |
B、 |
C、 |
D、 |
如图，已知点M、N分别为?ABCD的边CD、AB的中点，连接AM、CN．