题目内容
1．方程-5x2+5x+6=0的二次项系数是-5．分析 根据一元二次方程的一般形式是：ax2+bx+c=0（a，b，c是常数且a≠0）特别要注意a≠0的条件，a叫二次项系数，可得答案．
解答 解：-5x2+5x+6=0的二次项系数是-5，
故答案为：-5．
点评 本题考查了一元二次方程的一般形式，一元二次方程的一般形式是：ax2+bx+c=0（a，b，c是常数且a≠0）特别要注意a≠0的条件．这是在做题过程中容易忽视的知识点．在一般形式中ax2叫二次项，bx叫一次项，c是常数项．其中a，b，c分别叫二次项系数，一次项系数，常数项．
练习册系列答案
计算高手系列答案
相关题目
如图，△ABC，△ADE均为等边三角形，连接BD，CE，则线段BD与CE的数量关系是BD=CE．
16．抛物线y=-$\frac{1}{4}{（{x-\frac{1}{2}}）^2}$-5的顶点坐标是（ ）
| A． | $（\frac{1}{2}，-5）$ | B． | $（-5，-\frac{1}{2}）$ | C． | $（-\frac{1}{2}，-5）$ | D． | $（-\frac{1}{2}，5）$ |
画出下列几何体的三种形状图．
13．
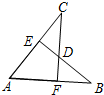如图，AB=AC，CF⊥AB于F，BE⊥AC于E，CF与BE交于点D．有下列结论：
①△ABE≌△ACF；②△BDF≌△CDE；③点D在∠BAC的平分线上．
以上结论正确的（ ）
如图，AB=AC，CF⊥AB于F，BE⊥AC于E，CF与BE交于点D．有下列结论：①△ABE≌△ACF；②△BDF≌△CDE；③点D在∠BAC的平分线上．
以上结论正确的（ ）
| A． | 只有① | B． | 只有② | C． | 只有③ | D． | 有①和②和③ |