题目内容
阅读下列解题过程，然后解题：
题目：已知
（a、b、c互不相等），求x+y+z的值．
解：设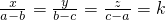
，则x=k（a-b），y=k（b-c），z=k（c-a），
∴x+y+z=k（a-b+b-c+c-a）=k•0=0，∴x+y+z=0．
依照上述方法解答下列问题：
已知：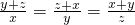
，其中x+y+z≠0，求
的值．
解：设
=
=
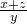=k，
则：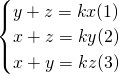
，
（1）+（2）+（3）得：2x+2y+2z=k（x+y+z），
∵x+y+z≠0，
∴k=2，
∴原式=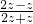
=
=
．
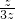分析：根据提示，先设比值为k，再利用等式列出三元一次方程组，即可求出k的值是2，然后把x+y=2z代入所求代数式．
点评：本题主要考查分式的基本性质，重点是设“k”法．
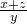===k，则：
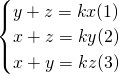，（1）+（2）+（3）得：2x+2y+2z=k（x+y+z），
∵x+y+z≠0，
∴k=2，
∴原式=
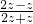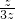==．分析：根据提示，先设比值为k，再利用等式列出三元一次方程组，即可求出k的值是2，然后把x+y=2z代入所求代数式．
点评：本题主要考查分式的基本性质，重点是设“k”法．
练习册系列答案
通城学典默写能手系列答案
相关题目