题目内容
已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10).(1)设△AMN的面积为y,求y关于t的函数关系解析式;
(2)求四边形MNBC的面积最小是多少?
(3)求时间t为何值时,△AMN是等腰三角形?

【答案】分析:(1)过N作NF⊥AC于F,求出OA=8,OB=6,AB=10,AC=10,根据sin∠BAC= =
= 求出NF=
求出NF= t,根据三角形面积公式求出即可;
t,根据三角形面积公式求出即可;
(2)根据y=- t2+3t=-
t2+3t=- (t-5)2+
(t-5)2+ ,求出△AMN的面积的最大值,根据三角形ABC的面积即可求出答案;
,求出△AMN的面积的最大值,根据三角形ABC的面积即可求出答案;
(3)AN=t,CM=t,AM=10-t,分为三种情况:①当AM=AN时,10-t=t,②当AM=MN时,作ME⊥AB于E,求出AE= (10-t),且AE=
(10-t),且AE= AN,得出方程
AN,得出方程 (10-t)=
(10-t)= t,求出方程的解即可;③当AN=MN时,过N作NF⊥AC于F,cos∠BAC=
t,求出方程的解即可;③当AN=MN时,过N作NF⊥AC于F,cos∠BAC= =
= 求出AF=
求出AF= t,且AM=2AF,得出方程10-t=
t,且AM=2AF,得出方程10-t= t,求出方程的解即可.
t,求出方程的解即可.
解答:解:(1) 如图1,过N作NF⊥AC于F,
如图1,过N作NF⊥AC于F,
∵A(8,0)、B(0,6),
∴OA=8,OB=6,
由勾股定理得:AB=10,
∵AB=AC,
∴AC=10,
sin∠BAC= =
= ,
,
∴ =
= ,
,
∴NF= t,
t,
∴y= ×AM×NF=
×AM×NF= •(10-t)•
•(10-t)• t,
t,
y=- t2+3t;
t2+3t;
(2)∵y=- t2+3t=-
t2+3t=- (t-5)2+
(t-5)2+ ,
,
∴△AMN的面积的最大值是 平方单位,
平方单位,
∴四边形MNBC的面积的最小值是S△ABC- =
= ×10×6-
×10×6- =
= 平方单位;
平方单位;
(3)根据已知得:AN=t,CM=t,AM=10-t,
分为三种情况:①当AM=AN时,10-t=t,
t=5;
②当AM=MN时,如图2,
作ME⊥AB于E,
cos∠BAC= =
= ,
,
∴ =
= ,
,
AE= (10-t),且AE=
(10-t),且AE= AN,
AN,
∴ (10-t)=
(10-t)= t,
t,
t= ;
;
③当AN=MN时,如图3,
过N作NF⊥AC于F,
cos∠BAC= =
= ,
,
∴ =
= ,
,
∴AF= t,且AM=2AF,
t,且AM=2AF,
∴10-t= t,
t,
t= ,
,
即时间t为5秒或 秒或
秒或 秒时,△AMN是等腰三角形.
秒时,△AMN是等腰三角形.
点评:本题考查了解直角三角形,三角形面积,二次函数的最值,等腰三角形的性质的应用,主要考查学生综合运用性质尽计算的能力,用了分类讨论思想.
 =
= 求出NF=
求出NF= t,根据三角形面积公式求出即可;
t,根据三角形面积公式求出即可;(2)根据y=-
 t2+3t=-
t2+3t=- (t-5)2+
(t-5)2+ ,求出△AMN的面积的最大值,根据三角形ABC的面积即可求出答案;
,求出△AMN的面积的最大值,根据三角形ABC的面积即可求出答案;(3)AN=t,CM=t,AM=10-t,分为三种情况:①当AM=AN时,10-t=t,②当AM=MN时,作ME⊥AB于E,求出AE=
 (10-t),且AE=
(10-t),且AE= AN,得出方程
AN,得出方程 (10-t)=
(10-t)= t,求出方程的解即可;③当AN=MN时,过N作NF⊥AC于F,cos∠BAC=
t,求出方程的解即可;③当AN=MN时,过N作NF⊥AC于F,cos∠BAC= =
= 求出AF=
求出AF= t,且AM=2AF,得出方程10-t=
t,且AM=2AF,得出方程10-t= t,求出方程的解即可.
t,求出方程的解即可.解答:解:(1)
 如图1,过N作NF⊥AC于F,
如图1,过N作NF⊥AC于F,∵A(8,0)、B(0,6),
∴OA=8,OB=6,
由勾股定理得:AB=10,
∵AB=AC,
∴AC=10,
sin∠BAC=
 =
= ,
,∴
 =
= ,
,∴NF=
 t,
t,∴y=
 ×AM×NF=
×AM×NF= •(10-t)•
•(10-t)• t,
t,y=-
 t2+3t;
t2+3t;(2)∵y=-
 t2+3t=-
t2+3t=- (t-5)2+
(t-5)2+ ,
,∴△AMN的面积的最大值是
 平方单位,
平方单位,∴四边形MNBC的面积的最小值是S△ABC-
 =
= ×10×6-
×10×6- =
= 平方单位;
平方单位;(3)根据已知得:AN=t,CM=t,AM=10-t,
分为三种情况:①当AM=AN时,10-t=t,
t=5;
②当AM=MN时,如图2,

作ME⊥AB于E,
cos∠BAC=
 =
= ,
,∴
 =
= ,
,AE=
 (10-t),且AE=
(10-t),且AE= AN,
AN,∴
 (10-t)=
(10-t)= t,
t,t=
 ;
;③当AN=MN时,如图3,

过N作NF⊥AC于F,
cos∠BAC=
 =
= ,
,∴
 =
= ,
,∴AF=
 t,且AM=2AF,
t,且AM=2AF,∴10-t=
 t,
t,t=
 ,
,即时间t为5秒或
 秒或
秒或 秒时,△AMN是等腰三角形.
秒时,△AMN是等腰三角形.点评:本题考查了解直角三角形,三角形面积,二次函数的最值,等腰三角形的性质的应用,主要考查学生综合运用性质尽计算的能力,用了分类讨论思想.

练习册系列答案
相关题目

 的图象的一个分支位于第一象限.
的图象的一个分支位于第一象限.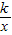 的图象的图象上,求k的值;
的图象的图象上,求k的值; S1?
S1?
 的图象与y轴交于点A,
的图象与y轴交于点A, 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐 时x的取值范围。
时x的取值范围。
 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
