题目内容

如图，在△ABC与△AEF中，∠AFE=90°，AB= $数学公式$ ，BC=5，AC= $数学公式$ ，AE=AC，延长FA交BC于点D．若∠ADC=∠CAE，则EF的长为________．

$\text{[math]}$
分析：作AH⊥BC于H点，由∠ADC=∠CAE，根据三角形外角性质得∠FAE=∠C，则可根据“AAS”判断△AEF≌△CAH，所以EF=AH，设HC=x，则BH=BC-CH=5-x，再根据勾股定理得到AH²+x²=（ $\text{[math]}$ ）²，AH²+（x-5）²=（2 $\text{[math]}$ ）²，然后解方程组求出AH，即可得到EF的长．
解答：作AH⊥BC于H点，如图，

∵∠ADC=∠CAE，∠FAC=∠ADC+∠C，
∴∠FAE=∠C，
在△AEF和△CAH中，
$\text{[math]}$ ，
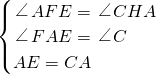∴△AEF≌△CAH（AAS），
∴EF=AH，
设HC=x，则BH=BC-CH=5-x，
在Rt△AHC中，
∵AH²+HC²=AC²，
∴AH²+x²=（ $\text{[math]}$ ）²①，
在Rt△AHB中，
∵AH²+HB²=AB²，
∴AH²+（x-5）²=（2 $\text{[math]}$ ）²②，
①-②得-25+10x=-5，解得x=3，
把x=2代入①得AH²+2²=（ $\text{[math]}$ ）²，解得AH= $\text{[math]}$ ，
∴EF= $\text{[math]}$ ．
故答案为 $\text{[math]}$ ．
点评：本题考查了全等三角形的判定与性质：判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”；全等三角形的对应边相等．也考查了勾股定理．