题目内容
 如图,已知:DE∥BC,CD是∠ACB的平分线,∠B=70°,∠ACB=60°.求∠EDC和∠BDC的度数.
如图,已知:DE∥BC,CD是∠ACB的平分线,∠B=70°,∠ACB=60°.求∠EDC和∠BDC的度数.分析:根据角平分线求出∠ECD=∠DCB=30°,根据三角形的内角和定理求出∠BDC即可;根据平行线性质得出∠EDC=∠DCB,代入求出即可.
解答:解:∵CD是∠ACB的平分线,∠ACB=60°,
∴∠ECD=∠DCB=
∠ACB=30°,
∴∠BDC=180°-∠ABC-∠DCB=180°-30°-70°=80°,
∵DE∥BC,
∴∠EDC=∠DCB=30°.
∴∠ECD=∠DCB=
| 1 |
| 2 |
∴∠BDC=180°-∠ABC-∠DCB=180°-30°-70°=80°,
∵DE∥BC,
∴∠EDC=∠DCB=30°.
点评:本题考查了三角形的内角和定理,平行线性质,角平分线定义的应用,主要考查学生的推理能力.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 如图,已知AB∥DE,AB=DE,AF=DC,求证:四边形BCEF是平行四边形.
如图,已知AB∥DE,AB=DE,AF=DC,求证:四边形BCEF是平行四边形.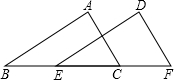 如图,已知AB=DE,AC=DF,要使△ABC≌△DEF,还需要补充一个条件,你补充的条件是:
如图,已知AB=DE,AC=DF,要使△ABC≌△DEF,还需要补充一个条件,你补充的条件是: 如图,已知:DE∥BC,AD:DB=1:2,DE=2,则BC=( )
如图,已知:DE∥BC,AD:DB=1:2,DE=2,则BC=( ) 如图,已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,请补充完整过程,说明△ABC≌△DEF的理由.
如图,已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,请补充完整过程,说明△ABC≌△DEF的理由.
 如图,已知AC∥DE,∠1=∠2.求证:AB∥CD.
如图,已知AC∥DE,∠1=∠2.求证:AB∥CD.