题目内容
解方程
(1)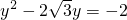
(2)(x-2)2=(2x+3)2
解:(1)化成一般形式为:
y2-2 y+2=0
y+2=0
a=1,b=-2 ,c=2
,c=2
b2-4ac= -4×1×2
-4×1×2
=12-8=4
y=
=
∴ ;
;
(2)把右边的项移到左边:(x-2)2-(2x+3)2=0
用平方差公式因式分解:(x-2+2x+3)(x-2-2x-3)=0
(3x+1)(-x-5)=0
3x+1=0或-x-5=0
∴ .
.
分析:(1)化成一般形式后,用公式法解;
(2)把右边的项移到左边,再用平方差公式因式分解来解方程.
点评:根据题目特点,寻找解方程的最佳方法.
y2-2
 y+2=0
y+2=0a=1,b=-2
 ,c=2
,c=2b2-4ac=
 -4×1×2
-4×1×2=12-8=4
y=

=

∴
 ;
;(2)把右边的项移到左边:(x-2)2-(2x+3)2=0
用平方差公式因式分解:(x-2+2x+3)(x-2-2x-3)=0
(3x+1)(-x-5)=0
3x+1=0或-x-5=0
∴
 .
.分析:(1)化成一般形式后,用公式法解;
(2)把右边的项移到左边,再用平方差公式因式分解来解方程.
点评:根据题目特点,寻找解方程的最佳方法.

练习册系列答案
相关题目