题目内容
 如图①两条直线交于一点,图中共有
如图①两条直线交于一点,图中共有| (4-2)×4 |
| 4 |
| (6-2)×6 |
| 4 |
| (8-2)×8 |
| 4 |
| (12-2)×12 |
| 4 |
| (12-2)×12 |
| 4 |
n2-n
n2-n
对对顶角.(用含n的式子表示)分析:根据提供的规律,对顶角的对数等于直线条数的2倍乘以2倍减2,然后除以4,进行计算即可得解.
解答:解:根据规律,六条直线交于一点,共有
=30对对顶角;
n条直线交于一点,共有
=n2-n对对顶角.
故答案为:
=30;n2-n.
| (12-2)×12 |
| 4 |
n条直线交于一点,共有
| (2n-2)•2n |
| 4 |
故答案为:
| (12-2)×12 |
| 4 |
点评:本题考查了对顶角的对数的变化规律,读懂题目信息,理解对顶角对数的求解方法是解题的关键.

练习册系列答案
相关题目
 (2013•株洲)已知抛物线C1的顶点为P(1,0),且过点(0,
(2013•株洲)已知抛物线C1的顶点为P(1,0),且过点(0, 已知抛物线C1的顶点为P(1,0),且过点(0,
已知抛物线C1的顶点为P(1,0),且过点(0, ).将抛物线C1向下平移h个单位(h>0)得到抛物线C2.一条平行于x轴的直线与两条抛物线交于A、B、C、D四点(如图),且点A、C关于y轴对称,直线AB与x轴的距离是m2(m>0).
).将抛物线C1向下平移h个单位(h>0)得到抛物线C2.一条平行于x轴的直线与两条抛物线交于A、B、C、D四点(如图),且点A、C关于y轴对称,直线AB与x轴的距离是m2(m>0). .
. ).将抛物线C1向下平移h个单位(h>0)得到抛物线C2.一条平行于x轴的直线与两条抛物线交于A、B、C、D四点(如图),且点A、C关于y轴对称,直线AB与x轴的距离是m2(m>0).
).将抛物线C1向下平移h个单位(h>0)得到抛物线C2.一条平行于x轴的直线与两条抛物线交于A、B、C、D四点(如图),且点A、C关于y轴对称,直线AB与x轴的距离是m2(m>0).
 .
. 对对顶角;如图②三条直线交于一
对对顶角;如图②三条直线交于一 对对顶角;如图③四条直线交于一点,图中共有
对对顶角;如图③四条直线交于一点,图中共有

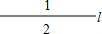 (1)一条直线可以把平面分成两个部分(或区域),如图,两条直线可以把平面分成几个部分?三条直线可以把平面分成几个部分?试画图说明.
(1)一条直线可以把平面分成两个部分(或区域),如图,两条直线可以把平面分成几个部分?三条直线可以把平面分成几个部分?试画图说明.