题目内容
 如图,E为?ABCD的边BC延长线上一点,AE与BD交于点F,与DC交于点G.
如图,E为?ABCD的边BC延长线上一点,AE与BD交于点F,与DC交于点G.
(1)写出所有与△ABE相似的三角形,并选择其中一对相似三角形加以证明;
(2)若BC=2CE,求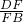 的值.
的值.
(3)若BC=k•CE,求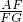 的值.
的值.
解:(1)△ABE∽△GCE∽△GDA;
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△ABE∽△GCE,△GCE∽△GDA,
∴△ABE∽△GCE∽△GDA;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△ADF∽△EBF,
∴ ,
,
∵BC=2CE,
∴AD:BE=2:3,
∴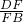 =
= ;
;
(3)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD∥BC,
∴△ECG∽△EBA,△ABF∽△GDF,
∴ ,
, ,
,
∵BC=k•CE,
∴ ,
,
∴ ,
,
∴ ,
,
∴ .
.
分析:(1)由四边形ABCD是平行四边形,可得AB∥CD,AD∥BC,平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似,即可得△ABE∽△GCE∽△GDA;
(2)易证得△ADF∽△EBF,根据相似三角形的对应边成比例可得 ,又由BC=2CE,即可求得
,又由BC=2CE,即可求得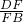 的值;
的值;
(3)易证得△ECG∽△EBA,△ABF∽△GDF,根据相似三角形的对应边成比例可得: ,
, ,又由BC=k•CE,即可求得
,又由BC=k•CE,即可求得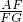 的值.
的值.
点评:此题考查了相似三角形的判定与性质以及平行四边形的性质.此题难度较大,注意掌握数形结合思想的应用,注意掌握平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似与相似三角形的对应边成比例定理的应用.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△ABE∽△GCE,△GCE∽△GDA,
∴△ABE∽△GCE∽△GDA;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△ADF∽△EBF,
∴
 ,
,∵BC=2CE,
∴AD:BE=2:3,
∴
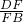 =
= ;
;(3)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD∥BC,
∴△ECG∽△EBA,△ABF∽△GDF,
∴
 ,
, ,
,∵BC=k•CE,
∴
 ,
,∴
 ,
,∴
 ,
,∴
 .
.分析:(1)由四边形ABCD是平行四边形,可得AB∥CD,AD∥BC,平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似,即可得△ABE∽△GCE∽△GDA;
(2)易证得△ADF∽△EBF,根据相似三角形的对应边成比例可得
 ,又由BC=2CE,即可求得
,又由BC=2CE,即可求得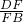 的值;
的值;(3)易证得△ECG∽△EBA,△ABF∽△GDF,根据相似三角形的对应边成比例可得:
 ,
, ,又由BC=k•CE,即可求得
,又由BC=k•CE,即可求得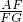 的值.
的值.点评:此题考查了相似三角形的判定与性质以及平行四边形的性质.此题难度较大,注意掌握数形结合思想的应用,注意掌握平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似与相似三角形的对应边成比例定理的应用.

练习册系列答案
相关题目
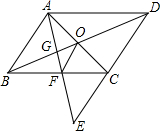 已知:如图,E为?ABCD中DC边的延长线上一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于O,连接OF,判断AB与OF的位置关系和大小关系,并证明你的结论.
已知:如图,E为?ABCD中DC边的延长线上一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于O,连接OF,判断AB与OF的位置关系和大小关系,并证明你的结论.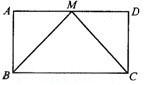 34、已知:如图,M为?ABCD的AD边上的中点,且MB=MC,
34、已知:如图,M为?ABCD的AD边上的中点,且MB=MC,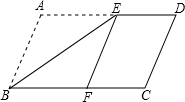 如图,E为?ABCD中AD边上的一点,将△ABE沿BE折叠使得点A刚好落在BC边上的F点处,若AB为4,ED为3,则?ABCD的周长为
如图,E为?ABCD中AD边上的一点,将△ABE沿BE折叠使得点A刚好落在BC边上的F点处,若AB为4,ED为3,则?ABCD的周长为 如图,E为?ABCD的边BC延长线上一点,AE与BD交于点F,与DC交于点G.
如图,E为?ABCD的边BC延长线上一点,AE与BD交于点F,与DC交于点G.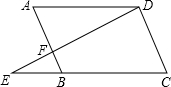 如图,E为?ABCD的边CB的延长线上一点,DE交AB于点F,则图中与△ADF相似的三角形是
如图,E为?ABCD的边CB的延长线上一点,DE交AB于点F,则图中与△ADF相似的三角形是