题目内容
(2012•云南)如图,在平面直角坐标系中,直线y=-
x+2交x轴于点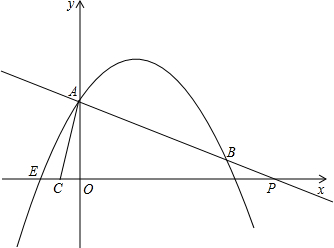 P,交y轴于点A.抛物线y=-
P,交y轴于点A.抛物线y=-
x2+bx+c的图象过点E(-1,0),并与直线相交于A、B两点.
(1)求抛物线的解析式(关系式);
(2)过点A作AC⊥AB交x轴于点C,求点C的坐标;
(3)除点C外,在坐标轴上是否存在点M,使得△MAB是直角三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
| 1 |
| 3 |
 P,交y轴于点A.抛物线y=-
P,交y轴于点A.抛物线y=-| 1 |
| 2 |
(1)求抛物线的解析式(关系式);
(2)过点A作AC⊥AB交x轴于点C,求点C的坐标;
(3)除点C外,在坐标轴上是否存在点M,使得△MAB是直角三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
分析:(1)首先求出A点坐标,然后利用待定系数法求出抛物线的解析式;
(2)利用相似三角形(Rt△OCA∽Rt△OPA)比例线段之间的关系,求出线段OC的长度,从而得到C点的坐标,如题图所示;
(3)存在所求的M点,在x轴上有3个,y轴上有2个,注意不要遗漏.求点M坐标的过程并不复杂,但要充分利用相似三角形比例线段之间的关系.
(2)利用相似三角形(Rt△OCA∽Rt△OPA)比例线段之间的关系,求出线段OC的长度,从而得到C点的坐标,如题图所示;
(3)存在所求的M点,在x轴上有3个,y轴上有2个,注意不要遗漏.求点M坐标的过程并不复杂,但要充分利用相似三角形比例线段之间的关系.
解答:解:(1)直线解析式为y=-
x+2,令x=0,则y=2,
∴A(0,2),
∵抛物线y=-
x2+bx+c的图象过点A(0,2),E(-1,0),
∴
,
解得
.
∴抛物线的解析式为:y=-
x2+
x+2.
(2)∵直线y=-
x+2分别交x轴、y轴于点P、点A,
∴P(6,0),A(0,2),
∴OP=6,OA=2.
∵AC⊥AB,OA⊥OP,
∴Rt△OCA∽Rt△OPA,∴
=
,
∴OC=
=
=
,
又C点在x轴负半轴上,
∴点C的坐标为C(-
,0).
(3)抛物线y=-
x2+
x+2与直线y=-
x+2交于A、B两点,
令-
x2+
x+2=-
x+2,
解得x1=0,x2=
,
∴B(
,
).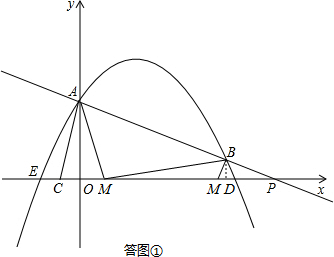
如答图①所示,过点B作BD⊥x轴于点D,
则D(
,0),BD=
,DP=6-
=
.
点M在坐标轴上,且△MAB是直角三角形,有以下几种情况:
①当点M在x轴上,且BM⊥AB,如答图①所示.
设M(m,0),则MD=
-m.
∵BM⊥AB,BD⊥x轴,∴
=
,
即
=
,
解得m=
,
∴此时M点坐标为(
,0);
②当点M在x轴上,且BM⊥AM,如答图①所示.
设M(m,0),则MD=
-m.
∵BM⊥AM,易知Rt△AOM∽Rt△MDB,
∴
=
,即
=
,
化简得:m2-
m+
=0,
解得:m1=
,m2=
,
∴此时M点坐标为(
,0),(
,0);
(说明:此时的M点相当于以AB为直径的圆与x轴的两个交点)
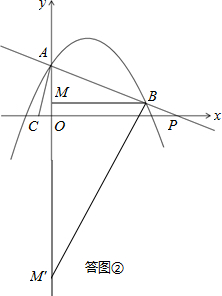
③当点M在y轴上,且BM⊥AM,如答图②所示.
此时M点坐标为(0,
);
④当点M在y轴上,且BM′⊥AB,如答图②所示.
设M′(0,m),则AM=2-
=
,BM=
,MM′=
-m.
易知Rt△ABM∽Rt△BM′M,
∴
=
,即
=
,
解得m=-
,
∴此时M点坐标为(0,-
).
综上所述,除点C外,在坐标轴上存在点M,使得△MAB是直角三角形.
符合条件的点M有5个,其坐标分别为:(
,0)、(
,0)、(
,0)、(0,
)或(0,-
).
| 1 |
| 3 |
∴A(0,2),
∵抛物线y=-
| 1 |
| 2 |
∴
|
解得
|
∴抛物线的解析式为:y=-
| 1 |
| 2 |
| 3 |
| 2 |
(2)∵直线y=-
| 1 |
| 3 |
∴P(6,0),A(0,2),
∴OP=6,OA=2.
∵AC⊥AB,OA⊥OP,
∴Rt△OCA∽Rt△OPA,∴
| OC |
| OA |
| OA |
| OP |
∴OC=
| OA2 |
| OP |
| 22 |
| 6 |
| 2 |
| 3 |
又C点在x轴负半轴上,
∴点C的坐标为C(-
| 2 |
| 3 |
(3)抛物线y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
令-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
解得x1=0,x2=
| 11 |
| 3 |
∴B(
| 11 |
| 3 |
| 7 |
| 9 |

如答图①所示,过点B作BD⊥x轴于点D,
则D(
| 11 |
| 3 |
| 7 |
| 9 |
| 11 |
| 3 |
| 7 |
| 3 |
点M在坐标轴上,且△MAB是直角三角形,有以下几种情况:
①当点M在x轴上,且BM⊥AB,如答图①所示.
设M(m,0),则MD=
| 11 |
| 3 |
∵BM⊥AB,BD⊥x轴,∴
| MD |
| BD |
| BD |
| DP |
即
| ||
|
| ||
|
解得m=
| 92 |
| 27 |
∴此时M点坐标为(
| 92 |
| 27 |
②当点M在x轴上,且BM⊥AM,如答图①所示.
设M(m,0),则MD=
| 11 |
| 3 |
∵BM⊥AM,易知Rt△AOM∽Rt△MDB,
∴
| OM |
| BD |
| OA |
| MD |
| m | ||
|
| 2 | ||
|

化简得:m2-
| 11 |
| 3 |
| 14 |
| 9 |
解得:m1=
11+
| ||
| 6 |
11-
| ||
| 6 |
∴此时M点坐标为(
11+
| ||
| 6 |
11-
| ||
| 6 |
(说明:此时的M点相当于以AB为直径的圆与x轴的两个交点)
③当点M在y轴上,且BM⊥AM,如答图②所示.
此时M点坐标为(0,
| 7 |
| 9 |
④当点M在y轴上,且BM′⊥AB,如答图②所示.
设M′(0,m),则AM=2-
| 7 |
| 9 |
| 11 |
| 9 |
| 11 |
| 3 |
| 7 |
| 9 |
易知Rt△ABM∽Rt△BM′M,
∴
| AM |
| BM |
| BM |
| MM′ |
| ||
|
| ||
|
解得m=-
| 92 |
| 9 |
∴此时M点坐标为(0,-
| 92 |
| 9 |
综上所述,除点C外,在坐标轴上存在点M,使得△MAB是直角三角形.
符合条件的点M有5个,其坐标分别为:(
| 92 |
| 27 |
11+
| ||
| 6 |
11-
| ||
| 6 |
| 7 |
| 9 |
| 92 |
| 9 |
点评:本题综合考查了二次函数的图象与性质、待定系数法求函数解析式、一次函数、解一元二次方程、相似三角形的判定与性质等重要知识点.难点在于第(3)问,所求的M点有5个(x轴上有3个,y轴上有2个),需要分情况讨论,不要遗漏.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•云南)如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.
(2012•云南)如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN. (2012•云南)如图,某同学在楼房的A处测得荷塘的一端B处的俯角为30°,荷塘另一端D与点C、B在同一直线上,已知AC=32米,CD=16米,求荷塘宽BD为多少米?(取
(2012•云南)如图,某同学在楼房的A处测得荷塘的一端B处的俯角为30°,荷塘另一端D与点C、B在同一直线上,已知AC=32米,CD=16米,求荷塘宽BD为多少米?(取 (2012•云南)如图,在△ABC中,∠C=90°,点D是AB边上的一点,DM⊥AB,且DM=AC,过点M作ME∥BC交AB于点E.
(2012•云南)如图,在△ABC中,∠C=90°,点D是AB边上的一点,DM⊥AB,且DM=AC,过点M作ME∥BC交AB于点E. (2012•云南)如图是由6个形同的小正方体搭成的一个几何体,则它的俯视图是( )
(2012•云南)如图是由6个形同的小正方体搭成的一个几何体,则它的俯视图是( )